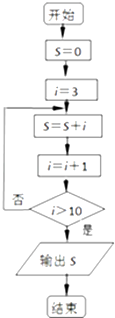
题目内容
【题目】已知在四棱锥P﹣ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E,F分别是线段AB,BC的中点. 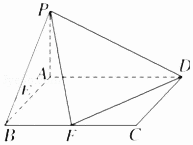
(1)证明:PF⊥FD;
(2)若PA=1,求点E到平面PFD的距离.
【答案】
(1)证明:连接AF,则AF= ![]() ,DF=
,DF= ![]() ,
,
又AD=2,∴DF2+AF2=AD2,∴DF⊥AF,
又PA⊥平面ABCD,∴DF⊥PA,又PA∩AF=A,
∴DF⊥平面PAF,
又PF平面PAF,
∴DF⊥PF.
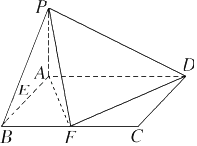
(2)解:∵S△EFD=2﹣ ![]() =
= ![]() ,
,
∴VP﹣EFD= ![]() =
= ![]() ,
,
∵VE﹣PFD=VP﹣AFD,
∴ ![]() ,解得h=
,解得h= ![]() ,即点E到平面PFD的距离为
,即点E到平面PFD的距离为 ![]() .
.
【解析】(1)连接AF,通过计算利用勾股定理证明DF⊥AF,证明DF⊥PA,推出DF⊥平面PAF,然后证明DF⊥PF.(2)利用等体积方法,求点E到平面PFD的距离.
【考点精析】通过灵活运用直线与平面垂直的性质,掌握垂直于同一个平面的两条直线平行即可以解答此题.

练习册系列答案
相关题目
【题目】濮阳市黄河滩区某村2010年至2016年人均纯收入(单位:万元)的数据如下表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(Ⅰ)求y关于x的线性回归方程;
(Ⅱ)利用(Ⅰ)中的回归方程,分析2010年至2016年该村人均纯收入的变化情况,并预测该村2017年人均纯收入.
附:回归直线的斜率和截距的最小乘法估计公式分别为: ![]() =
= 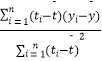 ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
.