题目内容
14.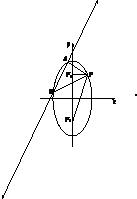 已知F1,F2是椭圆$\frac{x^2}{2}+\frac{y^2}{4}$=1的两焦点,P是椭圆在第一象限弧上一点,且满足$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$=1,若直线l:y=$\sqrt{2}$x+m(m∈(0,a]且a∈R)与椭圆交于A,B两点,
已知F1,F2是椭圆$\frac{x^2}{2}+\frac{y^2}{4}$=1的两焦点,P是椭圆在第一象限弧上一点,且满足$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$=1,若直线l:y=$\sqrt{2}$x+m(m∈(0,a]且a∈R)与椭圆交于A,B两点,(1)求点P的坐标;
(2)若△PAB的面积的最大值为$\frac{{\sqrt{6}}}{2}$,求实数a的值.
分析 (1)设出点P的坐标为(x0,y0)(x0>0,y0>0),由椭圆方程求得左右焦点坐标,然后结合$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}=1$求得P的坐标所满足的关系式,再根据P在椭圆上得另一关系式,联立即可求得P的坐标;
(2)联立直线方程和椭圆方程,化为关于x的一元二次方程后由判别式大于0求出m的范围,然后分别利用弦长公式和点到直线的距离公式求出弦AB的长及点P到直线AB的距离,代入三角形的面积公式后换元,然后利用二次函数的单调性求得最值,并由最大值为$\frac{{\sqrt{6}}}{2}$列式求实数a的值.
解答 解:(1)依题意,设点P的坐标为(x0,y0)(x0>0,y0>0),
由椭圆方程可得${F_1}(0,\sqrt{2})$,${F_2}(0,-\sqrt{2})$,
则$\overrightarrow{P{F}_{1}}=(-{x}_{0},\sqrt{2}-{y}_{0}),\overrightarrow{P{F}_{2}}=(-{x}_{0},-\sqrt{2}-{y}_{0})$,
∵$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}=1$,∴$(-{x_0},\sqrt{2}-{y_0})•$$(-{x_0},-\sqrt{2}-{y_0})=x_0^2-2+y_0^2=1$,
即$x_0^2+y_0^2=3$ ①,
又P是椭圆上一点,∴$\frac{x_0^2}{2}+\frac{y_0^2}{4}=1$,②
联立①②得,$x_0^2=1,y_0^2=2$,
又x0>0,y0>0,∴${x_0}=1,{y_0}=\sqrt{2}$.
故点P的坐标为$(1,\sqrt{2})$;
(2)∵直线AB的方程为$y=\sqrt{2}x+m$,
设A(x1,y1),B(x2,y2),
联立方程组$\left\{{\begin{array}{l}{y=\sqrt{2}x+m}\\{\frac{x^2}{2}+\frac{y^2}{4}=1}\end{array}}\right.$,消去y得$4{x^2}+2\sqrt{2}mx+{m^2}-4=0$.
∴${x_1}+{x_2}=-\frac{{\sqrt{2}}}{2}m$,${x_1}{x_2}=\frac{{{m^2}-4}}{4}$,
由△>0,得$m∈(-2\sqrt{2},2\sqrt{2})$,
又0<m≤a,则$0<a<2\sqrt{2}$.
点P(1,$\sqrt{2}$)到直线AB的距离为$d=\frac{|m|}{{\sqrt{3}}}$,
又$|{AB}|=\sqrt{3}\sqrt{{{({x_1}+{x_2})}^2}-4{x_1}{x_2}}=\sqrt{3(4-\frac{1}{2}{m^2})}$,
∴${S_{△PAB}}=\frac{1}{2}|{AB}|•d=\sqrt{\frac{1}{8}m{\;}^2(8-{m^2})}$.
令t=m2,则0<t≤a2,
∴${S_{△PAB}}=\sqrt{\frac{1}{8}t(8-t)}$,
令g(t)=t(8-t)(0<t≤a2),g(t)是二次函数,其图象是开口向下的抛物线,
对称轴为t=4,且g(4)=16.
又△PAB面积的最大值为$\frac{{\sqrt{6}}}{2}$时,g(t)也有最大值为12<g(4)=16,
故a2<4,
∴g(t)在(0,a2]单调递增,∴$g{(t)_{max}}=g({a^2})={a^2}(8-{a^2})=12$.
解得a2=2或a2=6(舍去).
∴当a2=2,即$a=\sqrt{2}$(满足$0<a<2\sqrt{2}$)时,△PAB面积的最大值为$\frac{{\sqrt{6}}}{2}$.
点评 本题考查了平面向量在解圆锥曲线问题中的应用,考查了直线和圆锥曲线的位置关系,涉及直线和圆锥曲线位置关系问题,常采用联立直线方程和圆锥曲线方程,然后利用一元二次方程的根与系数关系求解,该题还运用了换元法和函数的单调性求最值,综合性强.

| A. | $\sqrt{2}$-1 | B. | 2$\sqrt{2}$-2 | C. | 2-$\sqrt{2}$ | D. | 3-2$\sqrt{2}$ |
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | 0 |
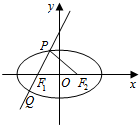 已知椭圆E的左、右焦点分别为F1、F2,过F1且斜率为2的直线交椭圆E于P、Q两点,若△PF1F2为直角三角形,则椭圆E的离心率为( )
已知椭圆E的左、右焦点分别为F1、F2,过F1且斜率为2的直线交椭圆E于P、Q两点,若△PF1F2为直角三角形,则椭圆E的离心率为( )| A. | $\frac{\sqrt{5}}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{\sqrt{2}}{3}$ | D. | $\frac{1}{3}$ |
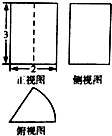 某由圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为60°的扇形,则该几何体的体积为( )
某由圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为60°的扇形,则该几何体的体积为( )| A. | 2π | B. | π | C. | $\frac{2π}{3}$ | D. | $\frac{π}{3}$ |