题目内容
2．已知点P为椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）上任意一点，F1、F2分别为椭圆的左、右焦点，I为△PF1F2的内心，若${S_{△PI{F_1}}}+{S_{△PI{F_2}}}=λ{S_{△{F_1}I{F_2}}}$成立，则λ的值为$\frac{a}{{\sqrt{{a^2}-{b^2}}}}$．分析 设出内接圆半径，把已知面积关系式，移项，利用椭圆的定义，即可求出λ的值．
解答 解：设内接圆的半径为r，因为${S_{△PI{F_1}}}+{S_{△PI{F_2}}}=λ{S_{△{F_1}I{F_2}}}$成立，
又椭圆的定义可知|PF1|+|PF2|=2a，|F1F2|=2c，
所以ar=λcr，c=$\sqrt{{a}^{2}-{b}^{2}}$，
所以λ=$\frac{a}{{\sqrt{{a^2}-{b^2}}}}$．
故答案为：$\frac{a}{{\sqrt{{a^2}-{b^2}}}}$．
点评 本题考查椭圆的定义，椭圆的基本性质的应用，考查分析问题解决问题的能力，比较基础．
练习册系列答案
精英口算卡系列答案
相关题目
5．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$的夹角为$\frac{π}{3}$，|$\overrightarrow{a}$|=1，且对任意实数x，不等式|x$\overrightarrow{a}$+2$\overrightarrow{b}$|≥|$\overrightarrow{a}$+$\overrightarrow{b}$|恒成立，则|$\overrightarrow{b}$|的取值范围是（ ）
| A． | [$\frac{1}{2}$，+∞） | B． | （$\frac{1}{2}$，+∞） | C． | [1，+∞） | D． | （1，+∞） |
17．
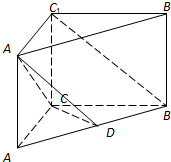如图所示，直三棱柱ABC-A1B1C1中，D是线段AB的中点，CA=CB=CC1=1，∠ACB=90°．
（1）证明：BC1∥面A1CD；
（2）求面A1CD与面A1C1CA所成的锐二面角的余弦值．
如图所示，直三棱柱ABC-A1B1C1中，D是线段AB的中点，CA=CB=CC1=1，∠ACB=90°．（1）证明：BC1∥面A1CD；
（2）求面A1CD与面A1C1CA所成的锐二面角的余弦值．
已知F1，F2是椭圆$\frac{x^2}{2}+\frac{y^2}{4}$=1的两焦点，P是椭圆在第一象限弧上一点，且满足$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$=1，若直线l：y=$\sqrt{2}$x+m（m∈（0，a]且a∈R）与椭圆交于A，B两点，
11．下列函数中是奇函数的是（ ）
| A． | y=$\frac{1}{x}$ | B． | y=x2+1 | C． | y=2x | D． | y=log2x |