题目内容
5．正四面体ABCD中，M，N分别是棱BC和棱AC的中点，则异面直线AM和DN所成的角的余弦值为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{6}$ | D． | 0 |
分析 画出立体图形，根据中点找平行线，把所求的异面直线角转化为一个三角形的内角来计算．
解答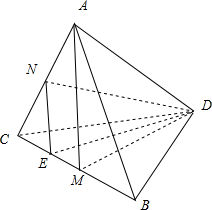 
解：如图，连接DM，取CM的中点E，连接DE，NE，则NE∥AM，故∠DNE即为所求的异面直线角．设这个正四面体的棱长为2，在△ABC中，AM=$\sqrt{3}$=DN=DM，EN=$\frac{1}{2}$AM=$\frac{\sqrt{3}}{2}$．
DE=$\sqrt{{EM}^{2}+{AM}^{2}}$=$\sqrt{\frac{1}{4}+3}$=$\frac{\sqrt{13}}{2}$．
∴cos∠END=$\frac{{EN}^{2}+{ND}^{2}-{DE}^{2}}{2NE•DN}$=$\frac{\frac{3}{4}+3-\frac{13}{4}}{2×\frac{\sqrt{3}}{2}×\sqrt{3}}$=$\frac{1}{6}$．
故选：C．
点评 本题考查空间点、线、面的位置关系及学生的空间想象能力、求异面直线角的能力．在立体几何中找平行线是解决问题的一个重要技巧，这个技巧就是通过三角形的中位线找平行线，如果试题的已知中涉及到多个中点，则找中点是出现平行线的关键技巧．
练习册系列答案
名校课堂系列答案
相关题目
5．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$的夹角为$\frac{π}{3}$，|$\overrightarrow{a}$|=1，且对任意实数x，不等式|x$\overrightarrow{a}$+2$\overrightarrow{b}$|≥|$\overrightarrow{a}$+$\overrightarrow{b}$|恒成立，则|$\overrightarrow{b}$|的取值范围是（ ）
| A． | [$\frac{1}{2}$，+∞） | B． | （$\frac{1}{2}$，+∞） | C． | [1，+∞） | D． | （1，+∞） |
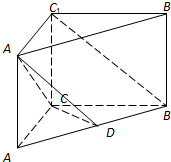如图所示，直三棱柱ABC-A1B1C1中，D是线段AB的中点，CA=CB=CC1=1，∠ACB=90°．
已知F1，F2是椭圆$\frac{x^2}{2}+\frac{y^2}{4}$=1的两焦点，P是椭圆在第一象限弧上一点，且满足$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$=1，若直线l：y=$\sqrt{2}$x+m（m∈（0，a]且a∈R）与椭圆交于A，B两点，