题目内容
4.已知点A(-2,0),B(0,-2),C(2sinθ,cosθ).(Ⅰ)若|$\overrightarrow{AC}$|=|$\overrightarrow{BC}$|,求tanθ和$\frac{3sinθ-4cosθ}{4cosθ+3sinθ}$的值;
(Ⅱ)若($\overrightarrow{OA}$+2$\overrightarrow{OB}$)•$\overrightarrow{OC}$=1,其中O为坐标原点,求sinθ•cosθ的值.
分析 (Ⅰ)由条件利用两个向量的数量积公式、同角三角函数的基本关系,求得2sinθ=cosθ,进一步化简求得tanθ和$\frac{3sinθ-4cosθ}{4cosθ+3sinθ}$的值.
(Ⅱ)由条件利用两个向量的数量积公式、同角三角函数的基本关系,求得sinθ+cosθ=-$\frac{1}{4}$,再平方,即可求得sinθ•cosθ的值.
解答 解:(Ⅰ)由题意可得,$\overrightarrow{AC}$=(2sinθ+2,cosθ),$\overrightarrow{BC}$=(2sinθ,cosθ+2),
若|$\overrightarrow{AC}$|=|$\overrightarrow{BC}$|,则 (2sinθ+2)2+cos2θ=(2sinθ)2+(cosθ+2)2,化简可得 2sinθ=cosθ,
∴tanθ=$\frac{1}{2}$,$\frac{3sinθ-4cosθ}{4cosθ+3sinθ}$=$\frac{3tanθ-4}{4+3tanθ}$=$\frac{\frac{3}{2}-4}{4+\frac{3}{2}}$=-$\frac{5}{11}$.
(Ⅱ)若($\overrightarrow{OA}$+2$\overrightarrow{OB}$)•$\overrightarrow{OC}$=(-2,-4)•(2sinθ,cosθ)=-4sinθ-4cosθ=1,
则 sinθ+cosθ=-$\frac{1}{4}$,平方可得 1+2sinθcosθ=$\frac{1}{16}$,∴sinθcosθ=-$\frac{15}{32}$.
点评 本题主要考查同角三角函数的基本关系,两个向量的数量积公式的应用,属于基础题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
12.函数y=f(x)为偶函数,满足f(x))=f(x-2),且当x∈[0,1]时,f(x)=x2,那么函数y=f(x)的图象与函数y=log4|x|的图象的交点共有( )
| A. | 6个 | B. | 4个 | C. | 3个 | D. | 2个 |
16.如表是某厂1-4月份用水量(单位:百吨)的一组数据:由散点图可知,用水量y与月份x之间有线性相关关系,其线性回归方程是$\widehat{y}$=-0.7x+$\widehat{a}$,则$\widehat{a}$=( )
| 月份x | 1 | 2 | 3 | 4 |
| 用水量y | 4.5 | 4 | 3 | 2.5 |
| A. | 5.15 | B. | 5.20 | C. | 5.25 | D. | 5.30 |
14.某几何体的三视图如图所示,则该几何体的外接球的体积为( )
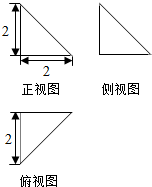

| A. | 4$\sqrt{3}$π | B. | $\frac{4\sqrt{3}π}{3}$ | C. | 4$\sqrt{2}$π | D. | $\frac{4\sqrt{2}π}{3}$ |
 已知F1,F2是椭圆$\frac{x^2}{2}+\frac{y^2}{4}$=1的两焦点,P是椭圆在第一象限弧上一点,且满足$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$=1,若直线l:y=$\sqrt{2}$x+m(m∈(0,a]且a∈R)与椭圆交于A,B两点,
已知F1,F2是椭圆$\frac{x^2}{2}+\frac{y^2}{4}$=1的两焦点,P是椭圆在第一象限弧上一点,且满足$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$=1,若直线l:y=$\sqrt{2}$x+m(m∈(0,a]且a∈R)与椭圆交于A,B两点,