题目内容
3．
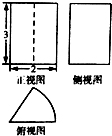某由圆柱切割获得的几何体的三视图如图所示，其中俯视图是中心角为60°的扇形，则该几何体的体积为（ ）| A． | 2π | B． | π | C． | $\frac{2π}{3}$ | D． | $\frac{π}{3}$ |
分析 由三视图知几何体为圆柱的一部分，且圆柱的高为3，底面圆的半径为2，根据正视图与俯视图可判断底面扇形的中心角为60°，求出圆柱的体积乘以$\frac{1}{6}$可得答案．
解答 解：由三视图知几何体为圆柱的一部分，且圆柱的高为3，底面圆的半径为2，
由正视图与俯视图判断底面扇形的中心角为60°，
∴几何体的体积V=$\frac{1}{6}$×π×22×3=2π，
故选：A．
点评 本题考查了由三视图求几何体的体积，解答的关键是判断几何体的形状及数据所对应的几何量．
练习册系列答案
相关题目
5．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$的夹角为$\frac{π}{3}$，|$\overrightarrow{a}$|=1，且对任意实数x，不等式|x$\overrightarrow{a}$+2$\overrightarrow{b}$|≥|$\overrightarrow{a}$+$\overrightarrow{b}$|恒成立，则|$\overrightarrow{b}$|的取值范围是（ ）
| A． | [$\frac{1}{2}$，+∞） | B． | （$\frac{1}{2}$，+∞） | C． | [1，+∞） | D． | （1，+∞） |
已知F1，F2是椭圆$\frac{x^2}{2}+\frac{y^2}{4}$=1的两焦点，P是椭圆在第一象限弧上一点，且满足$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$=1，若直线l：y=$\sqrt{2}$x+m（m∈（0，a]且a∈R）与椭圆交于A，B两点，
11．下列函数中是奇函数的是（ ）
| A． | y=$\frac{1}{x}$ | B． | y=x2+1 | C． | y=2x | D． | y=log2x |
8．已知f（x）是定义在R上的偶函数，若命题p：?x∈R，f（-x）=f（|x|），则?p为（ ）
| A． | ?x0∈R，f（-x0）≠f（|x0|） | B． | ?x∈R，f（-x）≠f（|x|） | ||
| C． | ?x0∈R，f（-x0）=f（|x0|） | D． | 不存在x0∈R，f（-x0）=f（|x0|） |