Question

【题目】已知函数，，其中

若函数，存在相同的零点，求a的值

若存在两个正整数m，n，当时，有与同时成立，求n的最大值及n取最大值时a的取值范围．

Answer 1

【答案】（Ⅰ）；（Ⅱ）.

【解析】

试题（Ⅰ）由函数可得其零点，代入函数可求得值；（Ⅱ）由和可得其解集交集，对进行分类讨论可得的最大整数为，此时的取值范围为.

试题解析：（Ⅰ）=，

∴，，

由得， 由得或或，

经检验上述的值均符合题意，所以的值为，，，；

（Ⅱ）令，则，∵为正整数，∴即，

记，令即的解集为， 则由题意得区间.

①当时，因为，故只能，

即或，又因为，故，此时.

又，所以.

当且仅当即时，可以取，

所以，的最大整数为；

②当时，，不合题意；

③当时，因为，，

故只能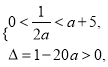无解；

综上，的最大整数为，此时的取值范围为．