题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)设函数![]() ,讨论函数
,讨论函数![]() 在区间
在区间![]() 内的零点个数;
内的零点个数;
(2)若对任意![]() ,总存在
,总存在![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)答案见解析;(2)![]() .
.
【解析】
(1)令![]() ,可得则
,可得则![]() ,简单判断
,简单判断![]() ,则
,则![]() ,作出函数
,作出函数![]() 与
与![]() 的图象,然后讨论
的图象,然后讨论![]() 的范围进而得解;
的范围进而得解;
(2)当![]() 时,
时,![]() ,则
,则![]() ,所以
,所以![]() 的值域是
的值域是![]() ;
;
当![]() 时,设函数
时,设函数![]() 的值域是
的值域是![]() ,依题意得
,依题意得![]() ,然后讨论
,然后讨论![]() 的范围进而得解.
的范围进而得解.
(1)因为![]() ,
,
令![]() ,
,
则![]() ,
,
当![]() 时,则
时,则![]() ,不符合条件,
,不符合条件,
当![]() 时,则
时,则![]()
作函数![]() 与
与![]() 的图象,由图可知:
的图象,由图可知:
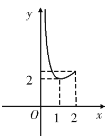
①当![]() 时,即
时,即![]() 时,两图象无公共点,
时,两图象无公共点,
则![]() 在区间
在区间![]() 内无零点;
内无零点;
②当![]() 时或
时或![]() 时,即
时,即![]() 或
或![]() 时,两图象仅有一个公共点,
时,两图象仅有一个公共点,
则![]() 在区间
在区间![]() 内仅有一个零点;
内仅有一个零点;
③当![]() 时,即
时,即![]() 时,两图象有两个公共点,
时,两图象有两个公共点,
则![]() 在区间
在区间![]() 内有两个零点.
内有两个零点.
(2)当![]() 时,
时,![]() ,则
,则![]() ,所以
,所以![]() 的值域是
的值域是![]() ;
;
当![]() 时,设函数
时,设函数![]() 的值域是
的值域是![]() ,依题意,
,依题意,![]() ,
,
①当![]() 时,
时,![]() 不合题意;
不合题意;
②当![]() 时,
时,![]() ,
,
由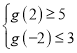 ,得
,得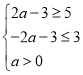 ,解得
,解得![]() ;
;
③当![]() 时,
时,![]() ,
,
由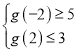 ,得
,得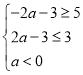 ,解得
,解得![]() ;
;
综上得,实数![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目


