题目内容
18.已知复数z=1+i+i2+…i10,则复数z在复平面内对应的点为( )| A. | (1,1) | B. | (1,-1) | C. | (0,1) | D. | (1,0) |
分析 找出规律1+i+i2+i3=0,计算即可.
解答 解:∵i2=-1,i3=-i,i4=1,
∴1+i+i2+i3=0,
i4+i5+i6+i7=i4(1+i+i2+i3)=0,
i8+i9+i10=i8(1+i+i2)=(1+i-1)=i,
∴z=1+i+i2+…i10=i,
其在复平面内对应的点为(0,1),
故选:C.
点评 本题考查虚数的运算,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
8.已知实数x∈[1,10]执行如图所示的流程图,则输出的x不小于63的概率为( )
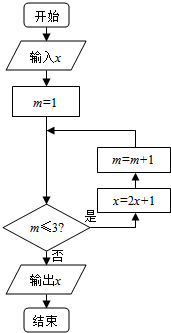

| A. | $\frac{1}{3}$ | B. | $\frac{4}{9}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{10}$ |
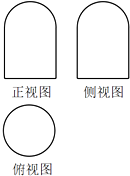 一个几何体的三视图如图,正视图和侧视图都是由一个半圆和一个边长为2的正方形组成,俯视图是一个圆,则这个几何体的表面积为7π.
一个几何体的三视图如图,正视图和侧视图都是由一个半圆和一个边长为2的正方形组成,俯视图是一个圆,则这个几何体的表面积为7π.