题目内容
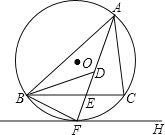
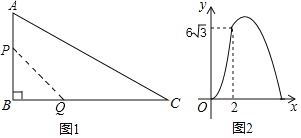
【题目】如图1,在△ABC中,∠B=90°,∠C=30°,动点P从点B开始沿边BA、AC向点C以恒定的速度移动,动点Q从点B开始沿边BC向点C以恒定的速度移动,两点同时到达点C,设△BPQ的面积为y(cm2).运动时间为x(s),y与x之间关系如图2所示,当点P恰好为AC的中点时,PQ的长为( )
A.2B.4C.2![]() D.4
D.4![]()
【答案】C
【解析】
点P、Q的速度比为3:![]() ,根据x=2,y=6
,根据x=2,y=6![]() ,确定P、Q运动的速度,即可求解.
,确定P、Q运动的速度,即可求解.
解:设AB=a,∠C=30°,则AC=2a,BC=![]() a,
a,
设P、Q同时到达的时间为T,
则点P的速度为![]() ,点Q的速度为
,点Q的速度为![]() ,故点P、Q的速度比为3:
,故点P、Q的速度比为3:![]() ,
,
故设点P、Q的速度分别为:3v、![]() v,
v,
由图2知,当x=2时,y=6![]() ,此时点P到达点A的位置,即AB=2×3v=6v,
,此时点P到达点A的位置,即AB=2×3v=6v,
BQ=2×![]() v=2
v=2![]() v,
v,
y=![]() AB×BQ=
AB×BQ=![]() 6v×2
6v×2![]() v=6
v=6![]() ,解得:v=1,
,解得:v=1,
故点P、Q的速度分别为:3,![]() ,AB=6v=6=a,
,AB=6v=6=a,
则AC=12,BC=6![]() ,
,
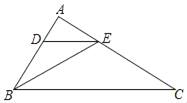
如图当点P在AC的中点时,PC=6,
此时点P运动的距离为AB+AP=12,需要的时间为12÷3=4,
则BQ=![]() x=4
x=4![]() ,CQ=BC﹣BQ=6
,CQ=BC﹣BQ=6![]() ﹣4
﹣4![]() =2
=2![]() ,
,
过点P作PH⊥BC于点H,

PC=6,则PH=PCsinC=6×![]() =3,同理CH=3
=3,同理CH=3![]() ,则HQ=CH﹣CQ=3
,则HQ=CH﹣CQ=3![]() ﹣2
﹣2![]() =
=![]() ,
,
PQ=![]() =
=![]() =2
=2![]() ,
,
故选:C.

【题目】已知![]() 是
是![]() 的函数,如表是
的函数,如表是![]() 与
与![]() 的几组对应值.
的几组对应值.
| … | ﹣5 | ﹣4 | ﹣3 | ﹣2 | 0 | 1 | 2 | 3 | 4 | 5 | … |
| … | 1.969 | 1.938 | 1.875 | 1.75 | 1 | 0 | ﹣2 | ﹣1.5 | 0 | 2.5 | … |
小明根据学习函数的经验,利用上述表格所反映出的![]() 与
与![]() 之间的变化规律,对该函数的图象与性质进行了探究.
之间的变化规律,对该函数的图象与性质进行了探究.
下面是小明的探究过程,请补充完整:

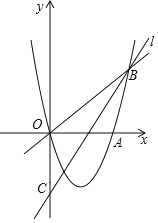
(1)如图,在平面直角坐标系![]() 中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(2)根据画出的函数图象,写出:
①![]() 对应的函数值
对应的函数值![]() 约为 ;
约为 ;
②该函数的一条性质: .