题目内容
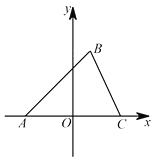
【题目】施工队要修建一个横断面为抛物线的公路隧道，其高度为6米，宽度OM为12米．现以O点为原点，OM所在直线为x轴建立直角坐标系（如图1所示）．
（1）求出这条抛物线的函数解析式，并写出自变量x的取值范围；
（2）隧道下的公路是双向行车道(正中间是一条宽1米的隔离带)，其中的一条行车道能否行驶宽2.5米、高5米的特种车辆？请通过计算说明；
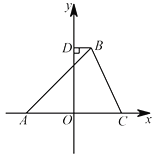
（3）施工队计划在隧道门口搭建一个矩形“脚手架”CDAB，使A、D点在抛物线上。B、C点在地面OM线上（如图2所示）．为了筹备材料，需测算“脚手架”三根钢杆AB、AD、DC的长度之和的最大值是多少，请你帮施工队计算一下.
【答案】（1）y=
；0≤x≤12 （2）不能行驶宽2.5米、高5米的特种车辆；（3）15
【解析】
试题（1）根据点P（6，6）为抛物线的顶点坐标可设这条抛物线的函数解析式为y=a(x－6)2+6，在根据图象经过原点即可求得结果；
（2）把x=6－0.5－2.5=3(或x=6+0.5+2.5=9)代入（1）中的函数关系式计算，结果与5比较即可判断.；
（3）设点A的坐标为（m，－
m2+2m），即可得到OB=m，AB=DC=－m2+2m，再根据抛物线的轴对称可得OB=CM=m，从而可以得到BC=12－2m，即AD=12－2m，即可得到L关于x的函数关系式，最后根据二次函数的性质即可求得结果.
（1）∵M（12，0），P（6，6）．
∴设这条抛物线的函数解析式为y=a(x－6)2+6，
∵把（0，0）代入解得a=－，
∴这条抛物线的函数解析式为y=－(x－6)2+6，
即y=－x2+2x（0≤x≤12）；
（2）当x=6－0.5－2.5=3(或x=6+0.5+2.5=9)时，y=4.5＜5
∴不能行驶宽2.5米、高5米的特种车辆；
（3）设点A的坐标为（m，－m2+2m），
∴OB=m，AB=DC=－m2+2m
根据抛物线的轴对称可得OB=CM=m，
∴BC=12－2m，即AD=12－2m
∴L=AB+AD+DC=－
m2+2m+12=－(m－3)2+15
∴当m=3，即OB=3米时，三根木杆长度之和L的最大值为15米．
