题目内容
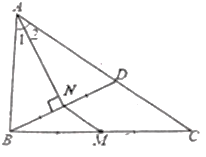
【题目】如图,BD是△ABC的角平分线,过点D作DE∥BC交AB于点E,DF∥AB交BC于点F.
(1)求证:四边形BEDF为菱形;
(2)如果∠A=90°,∠C=30°,BD=12,求菱形BEDF的面积.

【答案】(1)见解析;(2)24![]() .
.
【解析】
(1)根据平行四边形的和菱形的判定证明即可;
(2)根据含30°的直角三角形的性质和勾股定理以及菱形的面积解答即可.
证明:(1)∵DE∥BC,DF∥AB,
∴四边形BFDE是平行四边形,
∵BD是△ABC的角平分线,
∴∠EBD=∠DBF,
∵DE∥BC,
∴∠EDB=∠DBF,
∴∠EBD=∠EDB,
∴BE=ED,
∴平行四边形BFDE是菱形;
(2)连接EF,交BD于O,

∵∠BAC=90°,∠C=30°,
∴∠ABC=60°,
∵BD平分∠ABC,
∴∠DBC=30°,
∴BD=DC=12,
∵DF∥AB,
∴∠FDC=∠A=90°,
∴DF=![]() ,
,
在Rt△DOF中,OF=![]() ,
,
∴菱形BFDE的面积=![]() ×EFBD=
×EFBD=![]() ×12×4
×12×4![]() =24
=24![]() .
.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案【题目】“表1”为初三(1)班全部43名同学某次数学测验成绩的统计结果,则下列说法正确的是( )
成绩(分) | 70 | 80 | 90 |
男生(人) | 5 | 10 | 7 |
女生(人) | 4 | 13 | 4 |
A.男生的平均成绩大于女生的平均成绩
B.男生的平均成绩小于女生的平均成绩
C.男生成绩的中位数大于女生成绩的中位数
D.男生成绩的中位数小于女生成绩的中位数
【题目】某射击教练为了了解队员训练情况,从队员中选取甲、乙两名队员进行射击测试,相同条件下各射靶5次,成绩统计如下:
命中环数 | 6 | 7 | 8 | 9 | 10 |
甲命中相应环数的次数 | 0 | 1 | 3 | 1 | 0 |
乙命中相应环数的次数 | 2 | 0 | 0 | 2 | 1 |
(1)试通过计算说明甲、乙两人的成绩谁比较稳定?
(3)如果乙再射击1次,命中8环,那么乙射击成绩的方差会 .(填“变大”、“变小”或“不变”)