��Ŀ����
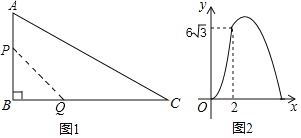
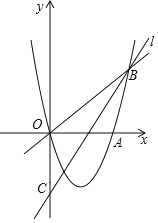
����Ŀ����ͼ��������y��ax2+bx+c����O��A��4��0����B��5��5�����㣬ֱ��l���������ڵ�B����y���ڵ�C��0����4������P����������һ�����㣮
��1���������ߵĽ���ʽ��
��2����P����ֱ��OB�ĶԳƵ�ǡ������ֱ��l�ϣ����P�����ꣻ
��3��M���߶�OB�ϵ�һ�����㣬����M��ֱ��MN��x�ᣬ���������ڵ�N������M��N��BΪ���������������OBC����ʱ��ֱ��д����N�����꣮
���𰸡���1�������߽���ʽΪ��y��x2��4x����2��P����![]() ��
��![]() ������3����N��������
������3����N��������![]() ����
����![]() ����
����![]() ����
����![]() ����
����
��������
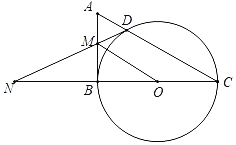
��1���������������߽���ʽΪy��ax��x��4������B��5��5��������ý���ʽ��
��2�������ֱ��BC����ʽ��OB����ʽ������ֱ��l����ֱ��OB�ԳƵ�ֱ�߽���ʽ���������������⣻
��3��������������ۣ������������ε������г���ʽ��������⣮
�⣺��1���������ߵĽ���ʽΪ��y��ax��x��4�����ҹ���B��5��5��
��5��5a
��a��1��
�������߽���ʽΪ��y��x��x��4����x2��4x��
��2������B��5��5������C��0����4����O��0��0��
��ֱ��BC����ʽΪ��y��![]() x��4��ֱ��OB����ʽΪ��y��x��
x��4��ֱ��OB����ʽΪ��y��x��
��C�㣨0��-4�����ɵ�C�����ֱ��OB�ĶԳƵ�Ϊ��-4��0��
��ֱ��l����ֱ��OB�ԳƵ�ֱ�߽���ʽΪy=kx+b,
�ѣ�-4��0������5��5�������![]()
���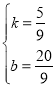
��ֱ��l����ֱ��OB�ԳƵ�ֱ�߽���ʽΪy��![]() ��
��
������������ɵã�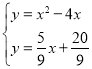
��![]() ��
��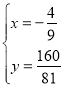
����P����![]() ��
��![]() ����
����
��3����ͼ��
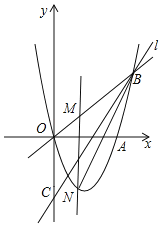
����B��5��5������C��0����4����O��0��0��
��OC��4��BO��![]() =5
=5![]() ����BOA��45����
����BOA��45����
���M��m��m�������N��m��m2��4m����
��MN��5m��m2��BM��![]() =
=![]() ��5��m����
��5��m����
��MN��y�ᣬ
���BMN����BOC����BOA +��COA =135����
����M��N��BΪ���������������OBC���ƣ�
�ٵ���BMN�ס�BOC
��![]() ��
��
��![]() ��
��![]() ��
��
��m1��5����ȥ����m2��![]() ��
��
����N��������![]() ����
����![]() ����
����
������BMN�ס�COB
��![]() ����
����![]() ��
��![]() ��
��
��m1��5����ȥ����m2��![]() ��
��
����N������![]() ����
����![]() ����
����
������������N��������![]() ����
����![]() ����
����![]() ����
����![]() ����
����

����Ŀ�������Կ�չ��ѧϰ��˼�룬���ýӰ����������Ķ���������ܵ���У�Ĺ㷺��ע��ͬѧ�ǵĻ�����Ӧ��ijУΪ�˽�ȫУѧ�������Ķ���������������˲���ѧ����ijһ�������Ķ����µ�ƪ�������Ƴ�����ͳ��ͼ��.
ijУ����ѧ�������Ķ���ƪ��ͳ�Ʊ�
�����Ķ���ƪ��(ƪ) | 3 | 4 | 5 | 6 | 7������ |
����(��) | 20 | 28 | m | 16 | 12 |

�����ͳ��ͼ���е���Ϣ�������������:
(1)����ѧ��������![]() ��ֵ��
��ֵ��
(2)�γ���ѧ�������Ķ�ƪ������λ����������
(3)����У����800��ѧ�������ݳ�������Ƹ�Уѧ������һ���������Ķ���ƪ��Ϊ4ƪ������.