Question

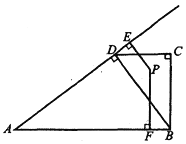
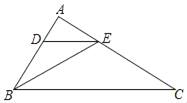
【题目】如图，在△ABC中，点D、E分别在边AB、AC上，AE2＝ADAB，∠ABE＝∠ACB．

（1）求证：DE∥BC；

（2）如果S△ADE：S四边形DBCE＝1：8，求S△ADE：S△BDE的值．

Answer 1

【答案】（1）见解析；（2）S△ADE：S△BDE=1：2.

【解析】

（1）根据已知条件得到，根据相似三角形的性质得到∠AED＝∠ABE，根据平行线的判定定理即可得到结论；

（2）根据相似三角形的性质得到，由已知条件得到，根据相似三角形的性质即可得到结论．

（1）证明：∵AE2＝ADAB，

∴，

又∵∠EAD＝∠BAE，

∴△AED∽△ABE，

∴∠AED＝∠ABE，

∵∠ABE＝∠ACB，

∴∠AED＝∠ACB，

∴DE∥BC；

（2）∵DE∥BC，

∴△ADE∽△ABC，

∴，

∵，

∴，

∴，

∴，

∴，

∴．