题目内容
【题目】某校初三（1）班 
名学生需要参加体育“五选一”自选项目测试，班上学生所报自选项目的情况统计表如下：
自选项目 | 人数 | 频率 |
立定跳远 | 9 | 0.18 |
三级蛙跳 | 12 |
|
一分钟跳绳 | 8 | 0.16 |
投掷实心球 |
| 0.32 |
推铅球 | 5 | 0.1 |
合计 | 50 | 1 |
（1）求 
的值；
（2）若将各自选项目的人数所占比例绘制成扇形统计图，求“一分钟跳绳”对应扇形的圆心角的度数；
（3）在选报“推铅球”的学生中，有3名男生，2名女生.为了了解学生的训练效果，从这5名学生中随机抽取两名学生进行推铅球测试，求所抽取的两名学生中至多有一名女生的概率.
【答案】
（1）
解：（1）根据题意得：a=1-（0.18+0.16+0.32+0.10）=0.24；
b=
×0.32=16
（2）
解：作出扇形统计图，如图所示：
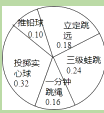
根据题意得：360°×0.16=57.6°；
（3）
解：男生编号为A、B、C，女生编号为D、E，
由枚举法可得：AB、AC、AD、AE、BC、BD、BE、CD、CE、DE共10种，其中DE为女女组合，
∴抽取的两名学生中至多有一名女生的概率为：P=
【解析】(1)根据表格求出a与b的值即可；
（2）根据表格做出扇形统计图，求出“一分钟跳绳”对应扇形的圆心角的度数即可；
（3）列表得出所有可能的情况数，找出抽取的两名学生中至多有一名女生的情况，即可求出概率。
【考点精析】通过灵活运用扇形统计图和列表法与树状图法，掌握能清楚地表示出各部分在总体中所占的百分比．但是不能清楚地表示出每个项目的具体数目以及事物的变化情况；当一次试验要设计三个或更多的因素时，用列表法就不方便了，为了不重不漏地列出所有可能的结果，通常采用树状图法求概率即可以解答此题．
练习册系列答案
相关题目
