Question

【题目】如图，顶点为（1，4）的抛物线 与直线 交于点A(2,2),直线 与 轴交于点B与 轴交于点C.

（1）求 的值及抛物线的解析式
（2）P为抛物线上的点，点P关于直线AB的对称轴点在 轴上，求点P的坐标
（3）点D为 轴上方抛物线上的一点，点E为轴上一点，以A 、B、E、D为顶点的四边为平行四边形时，直接写出点E的坐标。

Answer 1

【答案】
（1）

解：将A（2，2）代入y=x+n得n=1;

设抛物线的解析式y=a+4;

代入点A（2，2），可得a=-2;

所以抛物线的解析式y=-2+4=-2+4x+2;

（2）

解：如图1.设PP′与AC的交点为H，作HM⊥x轴于M，作PN⊥HM于N

设P(x,-2+4x+2),H(m,m+1)

∵H是PP′的中点，

∴NM=2HM;

∴-2+4x+2=m+2;

∴m=-2+4x ①;

又∵,NH=HM;

∴HM=2PN;

∴m+1=2(m-x),

∴4x=3m-2 ②;

联立① ②解得x=1或x=，

∴点P的坐标（1，4）(如图2）或（如图3）

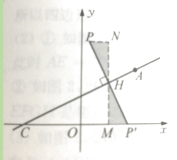
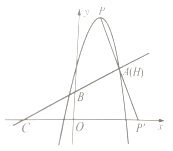
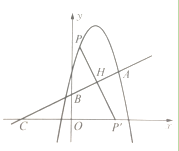
图1 图2 图3

（3）

解：设点E坐标为(t,0)，以AB为边或对角线进行分类讨论：

①如图4，当AB是平行四边行的边时，AB//DE,AB=DE;

∵点B(0,1)先向右平移2个单位，再向上平移1个单位得到A(2,2),

∴D(t+2，1）；

将D(t+2，1）代入y=-2+4，得-2+4=1;

解得t=或t=，

∴E(,0)(如图6）或E（，0）（如图5）

②如图7，当AB是平行四边形的对角线时，设AB的中点G(1,)，点E(t,0);

∴E关于G(1,)的对称点D的坐标可以表示为(2-t,3)

将D(2-t,3)代入y=-2+4，得-2+4=3;

解得t=或t=，

∴E(,0)（如图9）或E(,0)如图(5）

图4 图5 图6

【解析】(1)将A（2，2）代入y=x+n从而求出直线解析式，将抛物线解析式设成顶点坐标y=a+4代入A(2,2)从而求出抛物线解析式。
(2)如图1，设PP′与AC的交点为H，作HM⊥x轴于M，作PN⊥HM于N；由题意可列出方程组m=-2+4x ①;4x=3m-2 ②，联立即可得出答案。
(3)设点E坐标为(t,0)，以AB为边或对角线进行分类讨论即可得出答案。
【考点精析】解答此题的关键在于理解两点间的距离的相关知识，掌握同轴两点求距离，大减小数就为之．与轴等距两个点，间距求法亦如此．平面任意两个点，横纵标差先求值．差方相加开平方，距离公式要牢记，以及对菱形的性质的理解，了解菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半．