题目内容
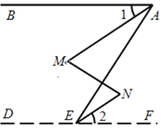
【题目】如图，AM∥BN，BC是∠ABN的平分线.
（1）过点A作AD⊥BC，垂足为O，AD与BN交于点D. （要求：用尺规作图，并在图中标明相应字母，保留作图痕迹，不写作法.）
（2）求证：AC=BD.
【答案】（1）图形见解析（2）证明见解析
【解析】
试题
（1）按“过直线外一点作已知直线的垂线的尺规作图方法”作出图形，并按要求标上相应字母即可；
（2）由BC平分∠ABN，AM∥BN可证得AB=AC；由AB=AC，AD⊥BC可得AD平分∠BAC，结合AM∥BN可证得AB=AD，从而可得BD=AC.
试题解析：
（1）如图3，AD为所求线段；
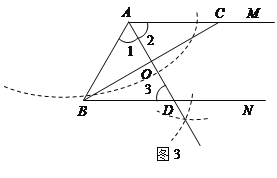
（2）∵ AM∥BN，
∴ ∠ACB=∠CBN.
∵ BC是∠ABN的平分线，
∴ ∠ABC=∠CBN，
∴ ∠ABC=∠ACB，
∴ AB=AC.
∵ AD⊥BC，∴ ∠1=∠2，
∵ AM∥BN，∴ ∠2=∠3，
∴ ∠1=∠3，
∴ AB=BD，
∴ AC=BD.
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
