题目内容
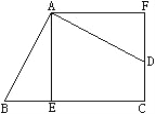
【题目】如图,为了开发利用海洋资源,某勘测飞机预测量一岛屿两端A、B的距离,飞机在距海平面垂直高度为100米的点C处测得端点A的俯角为60°,然后沿着平行于AB的方向水平飞行了500米,在点D测得端点B的俯角为45°,求岛屿两端A、B的距离(结果精确到0.1米,参考数据: ![]() )
)
【答案】解:过点A作AE⊥CD于点E,过点B作BF⊥CD于点F,
∵AB∥CD,
∴∠AEF=∠EFB=∠ABF=90°,
∴四边形ABFE为矩形.
∴AB=EF,AE=BF.
由题意可知:AE=BF=100米,CD=500米.
在Rt△AEC中,∠C=60°,AE=100米.
∴CE= ![]() =
= ![]() =
= ![]() (米).
(米).
在Rt△BFD中,∠BDF=45°,BF=100米.
∴DF= ![]() =
= ![]() =100(米).
=100(米).
∴AB=EF=CD+DF﹣CE=500+100﹣ ![]() ≈600﹣
≈600﹣ ![]() ×1.73≈600﹣57.67≈542.3(米).
×1.73≈600﹣57.67≈542.3(米).
答:岛屿两端A、B的距离为542.3米

【解析】首先过点A作AE⊥CD于点E,过点B作BF⊥CD于点F,易得四边形ABFE为矩形,根据矩形的性质,可得AB=EF,AE=BF.由题意可知:AE=BF=100米,CD=500米,然后分别在Rt△AEC与Rt△BFD中,利用三角函数即可求得CE与DF的长,继而求得岛屿两端A、B的距离.
【考点精析】掌握关于方向角问题是解答本题的根本,需要知道指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角.

练习册系列答案
相关题目