题目内容
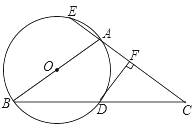
【题目】如图,二次函数 ![]() 的图象与x轴交于点 A,B,与y轴交于点C.点P是该函数图象上的动点,且位于第一象限,设点P的横坐标为x.
的图象与x轴交于点 A,B,与y轴交于点C.点P是该函数图象上的动点,且位于第一象限,设点P的横坐标为x.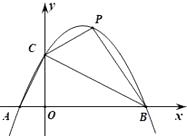
(1)写出线段AC,BC的长度:AC= , BC=;
(2)记△BCP的面积为S,求S关于x的函数表达式;
(3)过点P作PH⊥BC,垂足为H,连结AH,AP,设AP与BC交于点K,探究:是否存在四边形ACPH为平行四边形?若存在,请求出 ![]() 的值;若不存在,请说明理由,并求出
的值;若不存在,请说明理由,并求出 ![]() 的最大值.
的最大值.
【答案】
(1)解:AC= ![]() ,BC=
,BC= ![]()
(2)解:设P(x, ![]() ),则有
),则有 ![]()
= ![]() =
= ![]()
(3)解:过点P作PH⊥BC于H,
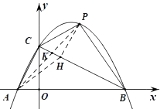
∵ ![]() ,
,
∴△ABC为直角三角形,即AC⊥BC;∴AC∥PH,
要使四边形ACPH为平行四边形,只需满足PH=AC= ![]() ,
,
∴ ![]() =5,而
=5,而 ![]() =
= ![]() =
= ![]() ,
,
所以不存在四边形ACPH为平行四边形
由△AKC∽△PHK,
∴ ![]() =
= ![]() (当x=2时,取到最大值)
(当x=2时,取到最大值)
【解析】(1)根据二次函数解析式写出A、B、C点的坐标,利用勾股定理即可得出AC、BC的长。
(2)求三角形的面积常用割补法,题解过程中,利用坐标系先进行补,在分割减法,即S = S Δ O C P + S Δ O B P S Δ O B C
(3)首先判定四边形是否存在,根据(2)求出PH长,和(1)中AC的长,得出对应边无法相等,所以四边形不存在,根据相似求出![]() 的值。
的值。

练习册系列答案
相关题目