题目内容
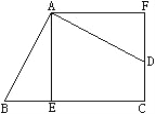
【题目】如图矩形ABCD中,AD=1,CD= ![]() ,连接AC,将线段AC、AB分别绕点A顺时针旋转90°至AE、AF,线段AE与弧BF交于点G,连接CG,则图中阴影部分面积为 .
,连接AC,将线段AC、AB分别绕点A顺时针旋转90°至AE、AF,线段AE与弧BF交于点G,连接CG,则图中阴影部分面积为 . 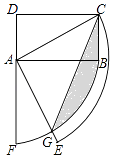
【答案】![]() ﹣
﹣ ![]()
【解析】解:在矩形ABCD中,
∵AD=1,CD= ![]() ,
,
∵AC=2,tan∠CAB= ![]() =
= ![]() ,
,
∴∠CAB=30°,
∵线段AC、AB分别绕点A顺时针旋转90°至AE、AF,
∴∠CAE=∠BAF=90°,
∴∠BAG=60°,
∵AG=AB= ![]() ,
,
∴阴影部分面积=S△ABC+S扇形ABG﹣S△ACG= ![]() ×
× ![]() ×1+
×1+ ![]() ﹣
﹣ ![]() ×
× ![]() ×2=
×2= ![]() ﹣
﹣ ![]() ,
,
所以答案是: ![]() ﹣
﹣ ![]() .
.
【考点精析】解答此题的关键在于理解矩形的性质的相关知识,掌握矩形的四个角都是直角,矩形的对角线相等,以及对扇形面积计算公式的理解,了解在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目