题目内容
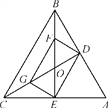
【题目】在△ABC中,AB=AC,点P为△ABC所在平面内一点,过点P分别作PE∥AC交AB于点E,PF∥AB交BC于点D,交AC于点F.
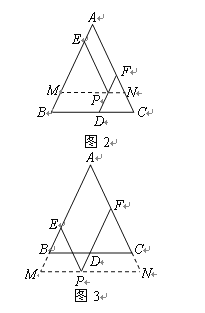
【1】如图1,若点P在BC边上,此时PD=0,易证PD,PE,PF与AB满足的数量关系PD+PE+PF=AB;当点P在△ABC内,先在图2中作出图形,并写出PD,PE,PF与AB满足的数量关系,然后证明你的结论
【2】当点P在△ABC外,先在图3中作出图形,然后写出PD,PE,PF与AB满足的数量关系.(不用说明理由)

【答案】
【1】结论:![]()
【2】![]()
【解析】重点考查四边形相关知识。利用等腰三角形和平行四边形的特性试运行解题。
解:(1)作图 …………………1分
结论:![]() …………………2分
…………………2分
证明:过点P作MN![]() BC
BC ![]()
![]() 四边形
四边形![]() 是平行四边形
是平行四边形 ![]() ………3分
………3分
![]()
![]() 四边形
四边形![]() 是平行四边形
是平行四边形
![]() ……………4分
……………4分 ![]()
![]()
又![]() ,MN
,MN![]() BC
BC
![]()
![]()
![]()
![]() …………………5分
…………………5分
![]()
![]() …………………6分
…………………6分
(2)作图 ……………7分
图3结论:

练习册系列答案
相关题目