题目内容
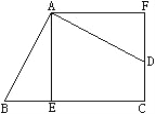
【题目】如图,∠BAE +∠AED=180°,∠1=∠2,那么∠M=∠N.下面是推理过程,请你完成.
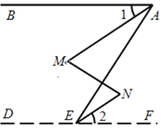
解:∵∠BAE+∠AED=180°(已知)
∴AB∥DE(______).
∴∠BAE=∠AEF(______).
又∵∠1=∠2(已知)
∴ ∠BAE∠1=∠AEF_____(等式性质),即 ∠MAE = ∠NEA .
∴_______∥______(______).
∴∠M=∠N(两直线平行,内错角相等).
【答案】见解析
【解析】
由已知易得AB∥CD,则∠BAE=∠AEC,又∠1=∠2,所以∠MAE=∠AEN,则AM∥EN,故∠M=∠N.
∵∠BAE+∠AED =180° (已知)
∴AB∥DE(同旁内角互补,两直线平行)
∴ ∠BAE=∠AEF (两直线平行,内错角相等).
又∵∠1=∠2(已知)
∴∠BAE ∠1 = ∠AEF ∠2(等式性质),即∠MAE=∠NEA .
∴AM∥EN(内错角相等,两直线平行).
∴∠M=∠N(两直线平行,内错角相等).
故答案为:同旁内角互补,两直线平行;两直线平行,内错角相等;∠2;AM;EN;内错角相等,两直线平行.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
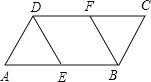
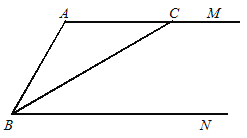
小学生10分钟应用题系列答案【题目】如图,AM∥BN,BC是∠ABN的平分线.
(1)过点A作AD⊥BC,垂足为O,AD与BN交于点D. (要求:用尺规作图,并在图中标明相应字母,保留作图痕迹,不写作法.)
(2)求证:AC=BD.
【题目】如图,△ABC中,AB= ![]() ,AC=5,tanA=2,D是BC中点,点P是AC上一个动点,将△BPD沿PD折叠,折叠后的三角形与△PBC的重合部分面积恰好等于△BPD面积的一半,则AP的长为 .
,AC=5,tanA=2,D是BC中点,点P是AC上一个动点,将△BPD沿PD折叠,折叠后的三角形与△PBC的重合部分面积恰好等于△BPD面积的一半,则AP的长为 . 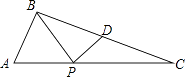
【题目】某班实行小组量化考核制,为了了解同学们的学习情况,王老师对甲、乙两个小组连续六周的综合评价得分进行了统计,并将得到的数据制成如下的统计表:
周次 组别 | 一 | 二 | 三 | 四 | 五 | 六 |
甲组 | 12 | 15 | 16 | 14 | 14 | 13 |
乙组 | 9 | 14 | 10 | 17 | 16 | 18 |
(1)请根据上表中的数据完成下表.(注:方差的计算结果精确到0.1)
平均数 | 中位数 | 方差 | |
甲组 | |||
乙组 |
(2)根据综合评价得分统计表中的数据,请在图中画出甲、乙两组综合评价得分的折线统计图.

(3)由折线统计图中的信息,请分别对甲、乙两个小组连续六周的学习情况进行简要评价.