题目内容
【题目】如图，排球运动员站在点M处练习发球，将球从M点正上方2m的A处发出，把球看成点，其运行的高度y（m）与运行的水平距离x（m）满足抛物线解析式．已知球达到最高2.6m的D点时，与M点的水平距离EM为6m．
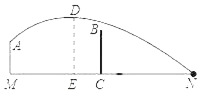
（1）在图中建立恰当的直角坐标系，并求出此时的抛物线解析式；
（2）球网BC与点M的水平距离为9m，高度为2.43m．球场的边界距M点的水平距离为18m．该球员判断此次发出的球能顺利过网并不会出界，你认为他的判断对吗？请说明理由．
【答案】（1）见解析，
；（2）该球员的判断不对，球会出界，见解析.
【解析】
（1）直角坐标系的建立要使点的坐标容易确定，因此可以以点M为坐标原点，建立平面直角坐标系，由题意即可确定点A，E，D的坐标，已知顶点D及抛物线上一点A的坐标，可设顶点式，利用待定系数法求解析式即可；（2）利用（1）所求解析式可求出球运行的高度和水平距离，与题中所给的球网BC的高度及球场的边界距M点的水平距离进行大小比较即可判断能否过网能否出界.
解：（1）如图，
以点M为坐标原点，建立平面直角坐标系，则点A，E，D的坐标分别为（0，2），（6，0），（6，2.6）
设球运行的高度y（m）与运行的水平距离x（m）的抛物线解析式为y＝a（x﹣h）2+k
由题意知抛物线的顶点为（6，2.6）
故y＝a（x﹣6）2+2.6
将点A（0，2）代入得2＝36a+2.6
∴a＝﹣
，
故此时抛物线的解析式为y＝﹣（x﹣6）2+2.6
（2）该球员的判断不对，理由如下：
当x＝9时，y＝﹣（x﹣6）2+2.6＝2.45＞2.43
∴球能过网；
当y＝0时，﹣（x﹣6）2+2.6＝0
解得：x1＝6+
＞18，x2＝6﹣（舍）
故球会出界．
练习册系列答案
相关题目
