题目内容
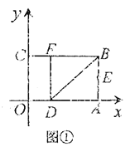
【题目】如图①,将一个矩形纸片![]() 放置在平面直角坐标系中,点
放置在平面直角坐标系中,点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() .点
.点![]() 是
是![]() 的中点,在
的中点,在![]() 上取一点
上取一点![]() ,将
,将![]() 沿
沿![]() 翻折,使点
翻折,使点![]() 落在
落在![]() 边上的点
边上的点![]() 处.
处.
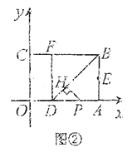
(Ⅰ)求点![]() 、
、![]() 的坐标;
的坐标;
(Ⅱ)如图②,若点![]() 是线段
是线段![]() 上的一个动点(点
上的一个动点(点![]() 不与点
不与点![]() ,
,![]() 重合),过点
重合),过点![]() 作
作![]() 于
于![]() ,设
,设![]() 的长为
的长为![]() ,
,![]() 的面积为
的面积为![]() ,试用关于
,试用关于![]() 的代数式表示
的代数式表示![]() ;
;
(Ⅲ)在![]() 轴、
轴、![]() 轴上分别存在点
轴上分别存在点![]() 、
、![]() ,使得四边形
,使得四边形![]() 的周长最小,请直接写出四边形
的周长最小,请直接写出四边形![]() 的周长最小值.
的周长最小值.
【答案】(Ⅰ)E(3,1),F(1,2);(Ⅱ)S=![]() -
-![]() +
+![]() ;(Ⅲ)5+
;(Ⅲ)5+![]() ;
;
【解析】
(Ⅰ)求出CF和AE的长度即可写出点的坐标;
(Ⅱ)用x表示出PD长度,结合三角函数进一步表示DH,PH的长度,运用三角形面积公式即可求解;
(Ⅲ)作点F关于y轴的对称点F′,点E关于x轴的对称点E′,连接E′F′交y轴于点N,交x轴于点M,此时四边形MNFE的周长最小,根据轴对称的性质可得四边形MNFE的周长=E′F′+EF,根据两点间的距离公式即可得出结论.
(Ⅰ)∵点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() ,
,
∴OA=3,AB=2
根据矩形OABC可得:AB=OC=2,BC=OA=3
由可翻折的性质可得:BF=AB=2,
∴CF=BC-BF=1,
∵点![]() 是
是![]() 的中点,∴AE=1,
的中点,∴AE=1,
∴E(3,1),F(1,2);
(Ⅱ)如图2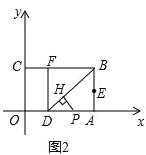
∵将△BDA沿BD翻折,使点A落在BC边上的点F处,
∴BF=AB=2,
∴OD=CF=3-2=1,
∵![]() =
=![]() ,OD=1,∴PD=x-1,
,OD=1,∴PD=x-1,
在Rt△ABD中,AB=2,AD=2,∴∠ADB=45°,
在Rt△PDH中,PH=DH=![]() DP=
DP=![]() (x-1),
(x-1),
∴S=![]() ×DH×PH=
×DH×PH=![]() ×
×![]() (x-1)×
(x-1)×![]() (x-1)=
(x-1)=![]() -
-![]() +
+![]() ;
;
(Ⅲ)如图3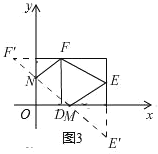
作点F关于y轴的对称点F′,点E关于x轴的对称点E′,连接E′F′交y轴于点N,交x轴于点M,此时四边形MNFE的周长最小,
∵点F(1,2)关于y轴的对称点F′(-1,2),
∵点E(3,1)关于x轴的对称点E′(3,-1),
∴F′N=FN, E′M=EM
∴四边形MNFE的周长=E′F′+EF=![]() ;
;
∴四边形MNFE周长的最小值为:![]() .
.

 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案【题目】学校举行图书节义卖活动,将所售款项捐给其他贫困学生.在这次义卖活动中,某班级售书情况如表:
售价 | 3元 | 4元 | 5元 | 6元 |
数目 | 14本 | 11本 | 10本 | 15本 |
下列说法正确的是( )
A. 该班级所售图书的总收入是226元
B. 在该班级所售图书价格组成的一组数据中,中位数是4
C. 在该班级所售图书价格组成的一纽数据中,众数是15
D. 在该班级所售图书价格组成的一组数据中,方差是2