Question

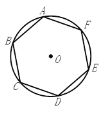
【题目】如图，六边形是⊙的内接正六边形，若正六边形的面积等于，则⊙的面积等于 __________ .

Answer 1

【答案】2π

【解析】

连接OE、OD，由正六边形的特点求出判断出△ODE的形状，作OH⊥ED，由特殊角的三角函数值求出OH的长，利用三角形的面积公式即可表示出△ODE的面积，进而根据正六边形ABCDEF的面积求得圆的半径，从而求得圆的面积．

连接OE、OD，

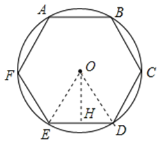
∵六边形ABCDEF是正六边形，
∴∠DEF=120°，
∴∠OED=60°，
∵OE=OD，
∴△ODE是等边三角形，
∴DE=OE，
设OE=DE=r，
作OH⊥ED交ED于点H，则sin∠OED=，
∴OH=r，
∵正六边形的面积等于3，
∴正六边形的面积=×rr×6=3，
解得：r=，
∴⊙O的面积等于2π，
故答案为：2π．