题目内容
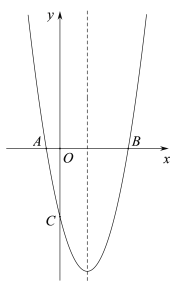
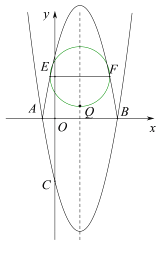
【题目】如图,抛物线![]() 的对称轴为直线x=2,抛物线与x轴交于点A和点B,与y轴交于点C,且点A的坐标为(-1,0).
的对称轴为直线x=2,抛物线与x轴交于点A和点B,与y轴交于点C,且点A的坐标为(-1,0).
(1)求抛物线的函数表达式;
(2)将抛物线![]() 图象x轴下方部分沿x轴向上翻折,保留抛物线在x轴上的点和x轴上方图象,得到的新图象与直线y=t恒有四个交点,从左到右四个交点依次记为D,E,F,G.当以EF为直径的圆过点Q(2,1)时,求t的值;
图象x轴下方部分沿x轴向上翻折,保留抛物线在x轴上的点和x轴上方图象,得到的新图象与直线y=t恒有四个交点,从左到右四个交点依次记为D,E,F,G.当以EF为直径的圆过点Q(2,1)时,求t的值;
(3)在抛物线![]() 上,当m≤x≤n时,y的取值范围是m≤y≤7,请直接写出x的取值范围.
上,当m≤x≤n时,y的取值范围是m≤y≤7,请直接写出x的取值范围.
【答案】(1)![]() ;(2)t的值为
;(2)t的值为![]() ;(3)x的取值范围是
;(3)x的取值范围是![]() 或
或![]() .
.
【解析】
(1)抛物线的对称轴是x=2,且过点A(-1,0)点,∴
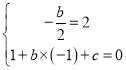 ,即可求解;
,即可求解;
(2)翻折后得到的部分函数解析式为:y=-(x-2)2+9=-x2+4x+5,(-1<x<5),新图象与直线y=t恒有四个交点,则0<t<9,由
![]() 解得:解得
解得:解得![]() ,
,![]() ,即可求解;
,即可求解;
(3)分m、n在函数对称轴左侧、m、n在对称轴两侧、m、n在对称轴右侧时,三种情况分别求解即可.
(1)抛物线的对称轴是x=2,且过点A(-1,0)点,∴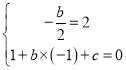 ,解得:
,解得:![]() ,
,
∴抛物线的函数表达式为:![]() ;
;
(2)解:∵![]() ,∴x轴下方图象翻折后得到的部分函数解析式为:
,∴x轴下方图象翻折后得到的部分函数解析式为:![]() =
=![]() (-1<x<5),其顶点为(2,9).
(-1<x<5),其顶点为(2,9).
∵新图象与直线y=t恒有四个交点,∴0<t<9.
设E(x1,y1),F(x2,y2).
由![]() 得
得![]() ,
,
解得![]() ,
,![]()
∵以EF为直径的圆过点Q(2,1),∴![]() ,
,
即![]() ,解得
,解得![]() .
.
又∵0<t<9,∴t的值为![]() ;
;
(3)x的取值范围是:![]() 或
或![]() .
.

练习册系列答案
相关题目