题目内容
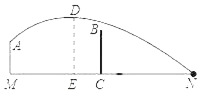
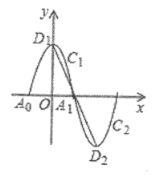
【题目】如图，一段抛物线
为
，与
轴交于
，
两点，顶点为
；将绕点旋转180°得到
，顶点为
；与组成一个新的图象.垂直于
轴的直线
与新图象交于点
，
，与线段交于点
，且
，
，
均为正数，设
，则
的最大值是（ ）
A. 15B. 18C. 21D. 24
【答案】B
【解析】
先求出
绕点
旋转180°得到
的解析式，再根据
，
，
均为正数且和最大，则可以得到l应在x轴的下方，根据二次函数的对称性可知x1+x2=12，由3≤x3≤6，推出x1+x2+x3的范围即可解决问题；
解：翻折后的抛物线的解析式为y=（x-6）2-9=x2-12x+27，
∵设x1，x2，x3均为正数，
∴点P1（x1，y1），P2（x2，y2）在第四象限，
根据对称性可知：x1+x2=12，
∵3≤x3≤6，
∴15≤x1+x2+x3≤18，即15≤t≤18，
∴
的最大值是18
故选：B．
练习册系列答案
相关题目
