题目内容
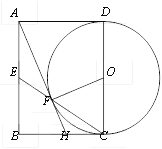
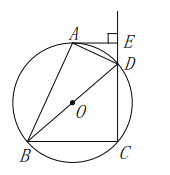
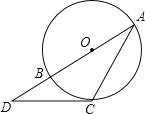
【题目】如图,O的直径AB=2,点D在AB的延长线上,DC与O相切于点C,连接AC.若∠A=30°,则CD长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
先连接BC,OC,由于AB 是直径,可知∠BCA=90°,而∠A=30°,易求∠CBA,又DC是切线,利用弦切角定理可知∠DCB=∠A=30°,再利用三角形外角性质可求∠D,再由切线的性质可得∠BCD=∠A=30°,∠OCD=90°,易得OD,由勾股定理可得CD.
如图所示,连接BC,OC,
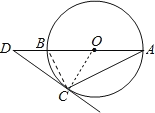
∵AB是直径,
∴∠BCA=90°,
又∵∠A=30°,
∴∠CBA=90°30°=60°,
∵DC是切线,
∴∠BCD=∠A=30°,∠OCD=90°,
∴∠D=∠CBA∠BCD=60°30°=30°,
∵AB=2,
∴OC=1,
∴OD=2,
∴CD=![]() ,
,
故选D.

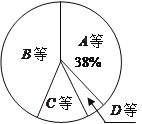
【题目】某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A、B、C、D四等,并绘制成下面的频数分布表和扇形统计图.
等第 | 成绩(得分) | 频数(人数) | 频率 |
A | 10分 | 7 | 0.14 |
9分 | x | m | |
B | 8分 | 15 | 0.30 |
7分 | 8 | 0.16 | |
C | 6分 | 4 | 0.08 |
5分 | y | n | |
D | 5分以下 | 3 | 0.06 |
合计 | 50 | 1.00 |
(1)试直接写出
(2)求表示得分为C等的扇形的圆心角的度数;
(3)如果该校九年级共有男生200名,试估计这200名男生中成绩达到A等和B等的人数共有多少人?
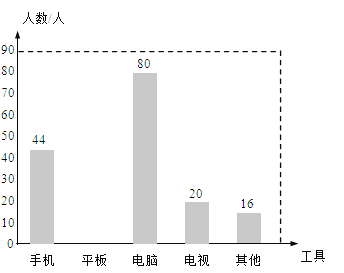
【题目】在“停课不停学”期间,某校数学兴趣小组对本校同学观看教学视频所使用的工具进行了调查,并从中随机抽取部分数据进行分析,将分析结果绘制成了两幅不完整的统计表与统计图.
工具 | 人数 | 频率 |
手机 | 44 | a |
平板 | b | 0.2 |
电脑 | 80 | c |
电视 | 20 | d |
不确定 | 16 | 0.08 |
请根据上述信息回答下列问题:
(1)所抽取出来的同学共 人,表中a= ,b= ;
(2)请补全条形统计图;
(3)若该校观看教学视频的学生总人数为2500人,则使用电脑的学生人数约 人.![]()
【题目】某年5月,我国南方某省A、B两市遭受严重洪涝灾害,1.5万人被迫转移,邻近县市C、D获知A、B两市分别急需救灾物资200吨和300吨的消息后,决定调运物资支援灾区.已知C市有救灾物资240吨,D市有救灾物资260吨,现将这些救灾物资全部调往A、B两市.已知从C市运往A、B两市的费用分别为每吨20元和25元,从D市运往往A、B两市的费用别为每吨15元和30元,设从D市运往B市的救灾物资为x吨.
(1)请填写下表
A(吨) | B(吨) | 合计(吨) | |
C |
|
| 240 |
D |
| x | 260 |
总计(吨) | 200 | 300 | 500 |
(2)设C、D两市的总运费为w元,求w与x之间的函数关系式,并写出自变量x的取值范围;
(3)经过抢修,从D市到B市的路况得到了改善,缩短了运输时间,运费每吨减少m元(m>0),其余路线运费不变.若C、D两市的总运费的最小值不小于10320元,求m的取值范围.