Question

【题目】[问题发现]

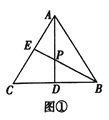
如图①，在中，点是的中点，点在边上，与相交于点，若，则_____ ;

[拓展提高]

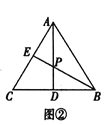
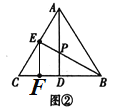
如图②，在等边三角形中，点是的中点，点在边上，直线与相交于点，若，求的值.

[解决问题]

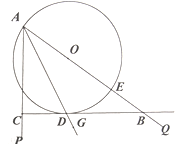
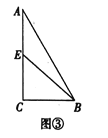
如图③，在中，，点是的中点，点在直线上，直线与直线相交于点，.请直接写出的长.

Answer 1

【答案】[问题发现]；[拓展提高]；[解决问题]或.

【解析】

[问题发现]由，可知AD是中线，则点P是△ABC的重心，即可得到2∶3；

[拓展提高]过点作交于点，则EF是△ACD的中位线，由平行线分线段成比例，得到，通过变形，即可得到答案；

[解决问题]根据题意，可分为两种情况进行讨论，①点D在点C的右边；②点D在点C的左边；分别画出图形，求出BP的长度，即可得到答案.

解：[问题发现]：∵，

∴点D是BC的中点，

∴AD是△ABC的中线，

∵点是的中点，则BE是△ABC的中线，

∴点P是△ABC的重心，

∴；

故答案为：.

[拓展提高]：过点作交于点.

是的中点，是的中点，

∴EF是△ACD的中位线，

，

，

，

∴，

，

即.

.

[解决问题]：∵在中，，，

∵点E是AC的中点，

∴，

∵CD=4，

则点D可能在点C的右边和左边两种可能；

①当点D在点C的右边时，如图：过点P作PF⊥CD与点F，

∵，，

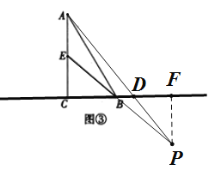
∴△ACD∽△PFD，

∴，即，

∴，

∵，，

∴△ECB∽△PBF，

∴，

∵，

∴，

解得：，

∴，，

∴；

②当点D在点C的左边时，如图：过点P作PF⊥CD与点F，

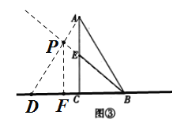
与①同理，可证△ACD∽△PFD，△ECB∽△PBF，

∴，，

∵，

∴，

解得：，

∴，，

∴；

∴或.