题目内容
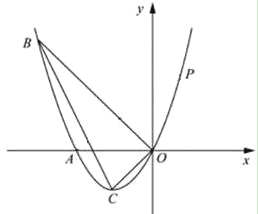
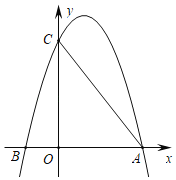
【题目】如图,平面直角坐标系中,抛物线y=﹣![]() (x﹣3a)(x+a)交x轴分别于点A、B(点B在x轴负半轴,OA>OB),交y轴于点C,OC=4OB,连接AC,点P从点A出发向点O运动,点Q从点A出发向点C运动.
(x﹣3a)(x+a)交x轴分别于点A、B(点B在x轴负半轴,OA>OB),交y轴于点C,OC=4OB,连接AC,点P从点A出发向点O运动,点Q从点A出发向点C运动.
(1)求a的值;
(2)点P、Q都以每秒1个单位的速度运动,运动t秒时,点A关于直线PQ对称的点E恰好在抛物线上,求t的值;
(3)点P以每秒1个单位的速度运动,点Q以每秒![]() 个单位的速度运动,直线PQ交抛物线于点M,当△CMA的内心在直线PQ上时,求点M的坐标.
个单位的速度运动,直线PQ交抛物线于点M,当△CMA的内心在直线PQ上时,求点M的坐标.
【答案】(1)a=1;(2)![]() ;(3)点M的坐标为(
;(3)点M的坐标为(![]() ,5)
,5)
【解析】
(1)由题意,可求得A(3a,0),B(﹣a,0),C(0,4a2),因为OC=4OB,得4a2=4a,即可得出a的值;
(2)作EH⊥AB于H,证明四边形PAQE为菱形,可得tan∠EPH=tan∠CAO=![]() ,设EH=4m,PH=3m,则PA=PE=5m,所以点E的坐标为(3﹣8m,4m),代入抛物线y=﹣
,设EH=4m,PH=3m,则PA=PE=5m,所以点E的坐标为(3﹣8m,4m),代入抛物线y=﹣![]() (x﹣3)(x+1),求得m的值,即可得出t的值;
(x﹣3)(x+1),求得m的值,即可得出t的值;
(3)连接MA,MC,作CH⊥MP于H,设运动时间为t秒,则AP=t,AQ=![]() ,可得PM∥CO,当△CMA的内心在直线PQ上时,证明△CHM∽△APM,得
,可得PM∥CO,当△CMA的内心在直线PQ上时,证明△CHM∽△APM,得![]() ,即
,即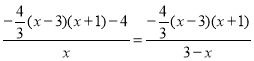 ,解方程求得x的值,即可得出点M的坐标.
,解方程求得x的值,即可得出点M的坐标.
解:(1)∵抛物线y=﹣![]() (x﹣3a)(x+a)交x轴分别于点A、B(点B在x轴负半轴,OA>OB),
(x﹣3a)(x+a)交x轴分别于点A、B(点B在x轴负半轴,OA>OB),
当y=0时,x=3a或x=﹣a,
当x=0时,y=4a2
∴A(3a,0),B(﹣a,0),C(0,4a2),
∵OC=4OB,
∴4a2=4a,
∴a=1或a=0(舍去),
∴a=1.
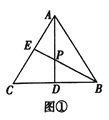
(2)如图1,作EH⊥AB于H,
∴点A关于直线PQ对称的点E恰好在抛物线上,
∴PA=PE,QA=QE,
∵AP=AQ=t,
∴PA=PE=QE=QA,
∴四边形PAQE为菱形,
∴EP∥AC,
∴∠EPH=∠CAO,
∵A(3,0),C(0,4),
∴tan∠EPH=tan∠CAO=![]() ,
,
设EH=4m,PH=3m,则PA=PE=5m,
∴点E的坐标为(3﹣8m,4m),
代入抛物线y=﹣![]() (x﹣3)(x+1),得4m=
(x﹣3)(x+1),得4m=![]() ×(﹣8m)×(4﹣8m),
×(﹣8m)×(4﹣8m),
∵m>0,解得m=![]() ,
,
∴t=5a=![]() ;
;
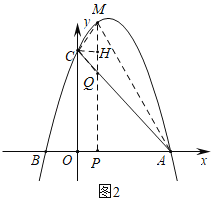
(3)如图2,连接MA,MC,作CH⊥MP于H,
设运动时间为t秒,则AP=t,AQ=![]() ,
,
∴![]() ,
,
∴PM∥CO,
当△CMA的内心在直线PQ上时,有∠CMH=∠AMP,
∵∠CHM=∠APM=90°,
∴△CHM∽△APM,
∴![]() ,
,
∴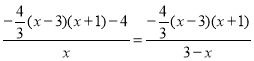 ,
,
化简,得![]() ,解得x=
,解得x=![]() ,
,
∴y=![]()
∴点M的坐标为(![]() ,5).
,5).

 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案