题目内容
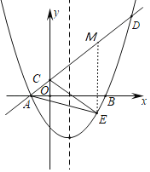
【题目】在平面直角坐标系中,将二次函数![]() 的图象向右平移1个单位,再向下平移2个单位,得到如图所示的抛物线,该抛物线与
的图象向右平移1个单位,再向下平移2个单位,得到如图所示的抛物线,该抛物线与![]() 轴交于点
轴交于点![]() 、
、![]() (点
(点![]() 在点
在点![]() 的左侧),
的左侧),![]() ,经过点
,经过点![]() 的一次函数
的一次函数![]() 的图象与
的图象与![]() 轴正半轴交于点
轴正半轴交于点![]() ,且与抛物线的另一个交点为
,且与抛物线的另一个交点为![]() ,
,![]() 的面积为5.
的面积为5.
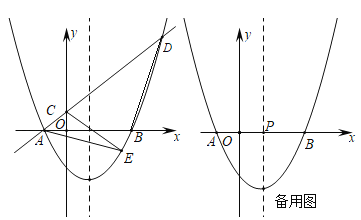
(1)求抛物线和一次函数的解析式;
(2)抛物线上的动点![]() 在一次函数的图象下方,求
在一次函数的图象下方,求![]() 面积的最大值,并求出此时点E的坐标;
面积的最大值,并求出此时点E的坐标;
(3)若点![]() 为
为![]() 轴上任意一点,在(2)的结论下,求
轴上任意一点,在(2)的结论下,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;
;![]() ;(2)
;(2)![]() 的面积最大值是
的面积最大值是![]() ,此时
,此时![]() 点坐标为
点坐标为![]() ;(3)
;(3)![]() 的最小值是3.
的最小值是3.
【解析】
(1)先写出平移后的抛物线解析式,再把点![]() 代入可求得
代入可求得![]() 的值,由
的值,由![]() 的面积为5可求出点
的面积为5可求出点![]() 的纵坐标,代入抛物线解析式可求出横坐标,由
的纵坐标,代入抛物线解析式可求出横坐标,由![]() 、
、![]() 的坐标可利用待定系数法求出一次函数解析式;
的坐标可利用待定系数法求出一次函数解析式;
(2)作![]() 轴交
轴交![]() 于
于![]() ,如图,利用三角形面积公式,由
,如图,利用三角形面积公式,由![]() 构建关于E点横坐标的二次函数,然后利用二次函数的性质即可解决问题;
构建关于E点横坐标的二次函数,然后利用二次函数的性质即可解决问题;
(3)作![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,则
,则![]() ,利用锐角三角函数的定义可得出
,利用锐角三角函数的定义可得出![]() ,此时
,此时![]() 最小,求出最小值即可.
最小,求出最小值即可.
解:(1)将二次函数![]() 的图象向右平移1个单位,再向下平移2个单位,得到的抛物线解析式为
的图象向右平移1个单位,再向下平移2个单位,得到的抛物线解析式为![]() ,
,
∵![]() ,∴点
,∴点![]() 的坐标为
的坐标为![]() ,
,
代入抛物线的解析式得,![]() ,∴
,∴![]() ,
,
∴抛物线的解析式为![]() ,即
,即![]() .
.
令![]() ,解得
,解得![]() ,
,![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∵![]() 的面积为5,∴
的面积为5,∴![]() ,∴
,∴![]() ,
,
代入抛物线解析式得,![]() ,解得
,解得![]() ,
,![]() ,∴
,∴![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,
,
∴ ,解得:
,解得:![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() .
.
(2)过点![]() 作
作![]() 轴交
轴交![]() 于
于![]() ,如图,设
,如图,设![]() ,则
,则![]() ,
,
∴![]() ,
,
∴![]()
![]() ,
,![]() ,
,
∴当![]() 时,
时,![]() 的面积有最大值,最大值是
的面积有最大值,最大值是![]() ,此时
,此时![]() 点坐标为
点坐标为![]() .
.
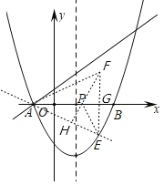
(3)作![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,连接
,连接![]() 交
交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,∴
,∴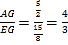 ,
,
∵![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∵![]() 、
、![]() 关于
关于![]() 轴对称,∴
轴对称,∴![]() ,
,
∴![]() ,此时
,此时![]() 最小,
最小,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
∴![]() 的最小值是3.
的最小值是3.

练习册系列答案
相关题目