题目内容
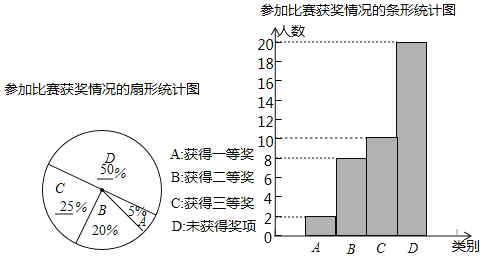
【题目】为纪念“五四运动”100周年,某校举行了征文比赛,该校学生全部参加了比赛.比赛设置一等、二等、三等三个奖项,赛后该校对学生获奖情况做了抽样调查,并将所得数据绘制成如图所示的两幅不完整的统计图.根据图中信息解答下列问题:
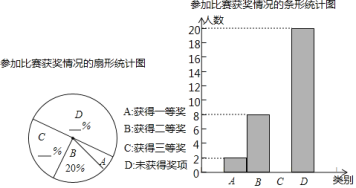
(1)本次抽样调查学生的人数为 .
(2)补全两个统计图,并求出扇形统计图中A所对应扇形圆心角的度数.
(3)若该校共有840名学生,请根据抽样调查结果估计获得三等奖的人数.
【答案】(1)40;(2)见解析,18°;(3)获得三等奖的有210人.
【解析】
(1)根据B的人数和所占的百分比可以求得本次抽样调查学生人数;
(2)根据统计图中的数据和(1)中的结果可以将统计图中所缺的数据补充完整并计算出扇形统计图中A所对应扇形圆心角的度数;
(3)根据统计图中的数据可以计算出获得三等奖的人数.
解:(1)本次抽样调查学生的人数为:8÷20%=40,
故答案为:40;
(2)A所占的百分比为:![]() ×100%=5%,
×100%=5%,
D所占的百分比为:![]() ×100%=50%,
×100%=50%,
C所占的百分比为:1﹣5%﹣20%﹣50%=25%,
获得三等奖的人数为:40×25%=10,
补全的统计图如图所示,
扇形统计图中A所对应扇形圆心角的度数是360°×5%=18°;
(3)840×25%=210(人),
答:获得三等奖的有210人.

练习册系列答案
相关题目