Question

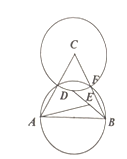
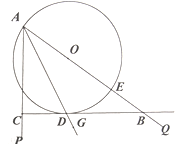
【题目】如图，AG是∠PAQ的平分线，点E在AQ上，以AE为直径的⊙0交AG于点D，过点D作AP的垂线，垂足为点C，交AQ于点B.

（1）求证：直线BC是⊙O的切线；

（2）若⊙O的半径为6，AC=2CD，求BD的长

Answer 1

【答案】（1）证明见详解；（2）8.

【解析】

（1）根据角平分线的定义和同圆的半径相等可得OD∥AC，证明OD⊥CB，可得结论；

（2））在Rt△ACD中，设CD=a，则AC=2a，AD=，证明△ACD∽△ADE，表示a=，由平行线分线段成比例定理得：，代入可得结论．

（1）证明：连接OD，

∵AG是∠HAF的平分线，

∴∠CAD=∠BAD，

∵OA=OD，

∴∠OAD=∠ODA，

∴∠CAD=∠ODA，

∴OD∥AC，

∵∠ACD=90°，

∴∠ODB=∠ACD=90°，即OD⊥CB，

∵D在⊙O上，

∴直线BC是⊙O的切线；

（2）解：在Rt△ACD中，设CD=a，则AC=2a，AD=，

连接DE，

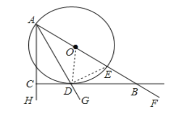
∵AE是⊙O的直径，

∴∠ADE=90°，

由∠CAD=∠BAD，∠ACD=∠ADE=90°，

∴△ACD∽△ADE，

∴,即，

∴，

由（1）知：OD∥AC，

解得BD=