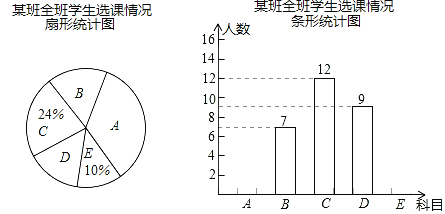
题目内容
【题目】如图,在平面直角坐标系中,抛物线y=x(x﹣b)﹣![]() 与y轴相交于A点,与x轴相交于B、C两点,且点C在点B的右侧,设抛物线的顶点为P.
与y轴相交于A点,与x轴相交于B、C两点,且点C在点B的右侧,设抛物线的顶点为P.
(1)若点B与点C关于直线x=1对称,求b的值;
(2)若OB=OA,求△BCP的面积;
(3)当﹣1≤x≤1时,该抛物线上最高点与最低点纵坐标的差为h,求出h与b的关系;若h有最大值或最小值,直接写出这个最大值或最小值.
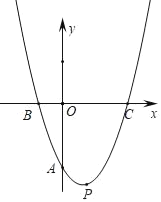
【答案】(1)2(2)![]() (3)h存在最小值,最小值为1
(3)h存在最小值,最小值为1
【解析】
(1)由点B与点C关于直线x=1对称,可得出抛物线的对称轴为直线x=1,再利用二次函数的性质可求出b值;
(2)利用二次函数图象上点的坐标特征可求出点A的坐标,结合OA=OB可得出点B的坐标,由点B的坐标利用待定系数法可求出抛物线的解析式,由抛物线的解析式利用二次函数图象上点的坐标特征可求出点C的坐标,利用配方法可求出点P的坐标,再利用三角形的面积公式即可求出△BCP的面积;
(3)分b≥2,0≤b<2,﹣2<b<0和b≤﹣2四种情况考虑,利用二次函数图象上点的坐标特征结合二次函数的图象找出h关于b的关系式,再找出h的最值即可得出结论.
解:(1)∵点B与点C关于直线x=1对称,y=x(x﹣b)﹣![]() =x2﹣bx﹣
=x2﹣bx﹣![]() ,
,
∴﹣![]() =1,
=1,
解得:b=2.
(2)当x=0时,y=x2﹣bx﹣![]() =﹣
=﹣![]() ,
,
∴点A的坐标为(0,﹣![]() ).
).
又∵OB=OA,
∴点B的坐标为(﹣![]() ,0).
,0).
将B(﹣![]() ,0)代入y=x2﹣bx﹣
,0)代入y=x2﹣bx﹣![]() ,得:0=
,得:0=![]() +
+![]() b﹣
b﹣![]() ,
,
解得:b=![]() ,
,
∴抛物线的解析式为y=x2﹣![]() x﹣
x﹣![]() .
.
∵y=x2﹣![]() x﹣
x﹣![]() =(x﹣
=(x﹣![]() )2﹣
)2﹣![]() ,
,
∴点P的坐标为(![]() ,﹣
,﹣![]() ).
).
当y=0时,x2﹣![]() x﹣
x﹣![]() =0,
=0,
解得:x1=﹣![]() ,x2=1,
,x2=1,
∴点C的坐标为(1,0).
∴S△BCP=![]() ×[1﹣(﹣
×[1﹣(﹣![]() )]×|﹣
)]×|﹣![]() |=
|=![]() .
.
(3)y=x2﹣bx﹣![]() =(x﹣
=(x﹣![]() )2﹣
)2﹣![]() ﹣
﹣![]() .
.
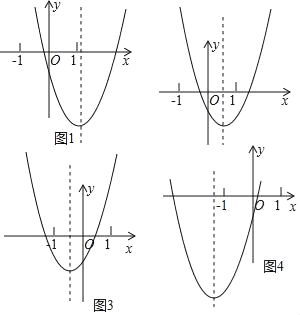
当![]() ≥1,即b≥2时,如图1所示,
≥1,即b≥2时,如图1所示,
y最大=b+![]() ,y最小=﹣b+
,y最小=﹣b+![]() ,
,
∴h=2b;
当0≤![]() <1,即0≤b<2时,如图2所示,
<1,即0≤b<2时,如图2所示,
y最大=b+![]() ,y最小=﹣
,y最小=﹣![]() ﹣
﹣![]() ,
,
∴h=1+b+![]() =(1+
=(1+![]() )2;
)2;
当﹣1<![]() <0,﹣2<b<0时,如图3所示
<0,﹣2<b<0时,如图3所示
y最大=![]() ﹣b,y最小=﹣
﹣b,y最小=﹣![]() ﹣
﹣![]() ,
,
∴h=1﹣b+![]() =(1﹣
=(1﹣![]() )2;
)2;
当![]() ≤﹣1,即b≤﹣2时,如图4所示,
≤﹣1,即b≤﹣2时,如图4所示,
y最大=﹣b+![]() ,y最小=b+
,y最小=b+![]() ,
,
h=﹣2b.
综上所述:h=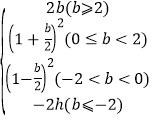 ,h存在最小值,最小值为1.
,h存在最小值,最小值为1.