题目内容
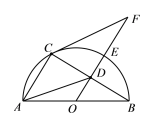
【题目】如图,AC为圆O的直径,弦AD的延长线与过点C的切线交于点B,E为BC中点,AC= ![]() ,BC=4.
,BC=4.
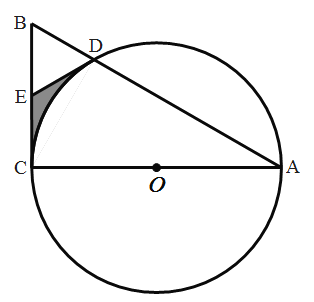
(1)求证:DE为圆O的切线;
(2)求阴影部分面积.
【答案】(1)证明见解析;(2)S阴影=4![]() -2π
-2π
【解析】
(1)根据斜边中线等于斜边一半得到DE=CE,再利用切线的性质得到∠BCO=90°,最后利用等量代换即可证明,(2)根据S阴影=2S△ECO-S扇形COD即可求解.
(1)连接DC、DO.
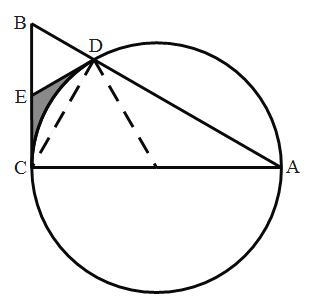
因为AC为圆O直径,
所以∠ADC=90°,则∠BDC=90°,
因为E为Rt△BDC斜边BC中点,
所以DE=CE=BE=![]() BC,
BC,
所以∠DCE=∠EDC,
因为OD=OC,
所以∠DCO=∠CDO.
因为BC为圆O 切线,
所以BC⊥AC,即∠BCO=90°,
所以∠ODE=∠ODC+∠EDC=∠OCD+∠DCE=∠BCO=90°,
所以ED⊥OD,
所以DE为圆O的切线.
(2)S阴影=2S△ECO-S扇形COD=4![]() -2π
-2π

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案【题目】在生活中,有很多函数并不一定存在解析式,对于这样的函数,我们可以通过列表和图象来对它可能存在的性质进行探索,例如下面这样一个问题:
已知y是x的函数,下表是y与x的几组对应值.
x | … | ﹣5 | ﹣4 | ﹣3 | ﹣2 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 1.969 | 1.938 | 1.875 | 1.75 | 1 | 0 | ﹣2 | ﹣1.5 | 0 | 2.5 | … |
小孙同学根据学习函数的经验,利用上述表格反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
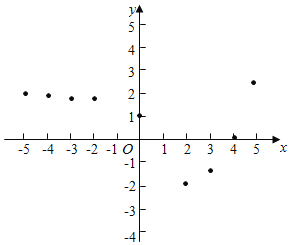
下面是小孙同学的探究过程,请补充完整;
(1)如图,在平面之间坐标系xOy中,描出了以上表中各对应值为坐标的点,根据描出的点,画出函数的图象:
(2)根据画出的函数图象回答:
①x=﹣1时,对应的函数值y的为 ;
②若函数值y>0,则x的取值范围是 ;
③写出该函数的一条性质(不能与前面已有的重复): .