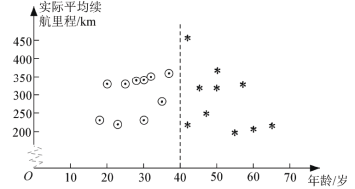
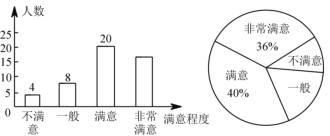��Ŀ����
����Ŀ��ij�꼶���� 150 ��Ů����Ϊ�˽���꼶Ů��ʵ����ɼ�����λ���ף���һ�������������ɼ�����λ����������������������ȡ 30 ��Ů�����в��ԣ���������ǵ���سɼ����������ݽ�������������������˲�����Ϣ��
a��ʵ����ɼ���Ƶ���ֲ������ʾ��

b��ʵ����ɼ��� 7.0��x��7.4 ��һ����ǣ�7.0��7.0��7.0��7.1��7.1��7.1��7.2��7.2��7.3��7.3
c��һ�������������ɼ���ͼ��ʾ��
����������Ϣ���ش��������⣺
��1���ٱ��� m ��ֵΪ ����һ�������������ɼ�����λ��Ϊ ��
��2����ʵ����ɼ��ﵽ 7.2 ������ʱ���ɼ���Ϊ���㣮
�������ȫ�꼶Ů��ʵ����ɼ��ﵽ�����������
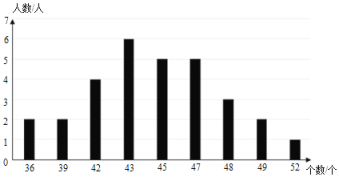
�ڸ��꼶ij������ίԱ����������γ��������б���ȡ�� 8 ��Ů��������ɼ������ݳ�¼�����ʾ��

������ 3 ��Ů����һ�������������ɼ�δ��¼����������ʦ˵�� 8 ��Ů����ǡ����4 ��������Գɼ����ﵽ�����㣬��������ίԱ�Ʋ�Ů�� E ��һ�������������ɼ��ﵽ�����㣬���Ƿ�ͬ������ίԱ��˵���� ����������������������
���𰸡���1��9��45����2��65����
��������
(1)�ٸ����ܳ������Ϊ30�ˣ���ȥ���������������ɵõ�m��ֵ���ڸ�������ͳ��ͼ�����ݺ���λ���Ķ�����Եõ��������ݵ���λ����
(2)���ȼ���������30������ɼ�������������ٹ���ȫ�꼶Ů��ʵ����ɼ��ﵽ������������ɵõ��𰸣��ڸ�������ͱ����е����ݿ��Խ���⣮
�⣺(1)��m=30-2-10-6-2-1=9����m��ֵ��9��
��������ͳ��ͼ�ɵã�
�����������ɼ���С�������к�15��16��ͬѧ�ijɼ�����45��
��һ�������������ɼ�����λ��Ϊ45��
�ʴ�Ϊ��9��45��
(2)�ٸ������⣬�����30�������棬�ﵽ���������Ϊ��4+6+2+1=13���ˣ���
�ʹ���ȫ�꼶Ů��ʵ����ɼ��ﵽ���������Ϊ��![]() ��
��
��ȫ�꼶Ů��ʵ����ɼ��ﵽ�������65�ˣ�
��ͬ�⣬
���ɣ����Ů��E�����������ɼ�δ�������㣬��ôֻ��A��D��F�п���������Գɼ����ﵽ���㣬����ǡ��4��������ɼ����ﵽ���㣬ì�ܣ���ˣ�Ů��E��һ�������������ɼ��ﵽ�����㣮

 ���ٴ���������ѧϰ����ѧ�ں����ν�ϵ�д�
���ٴ���������ѧϰ����ѧ�ں����ν�ϵ�д�