题目内容
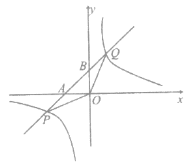
【题目】如图，反比例函数
的图象与一次函数
的图象交于点
和
两点，记一次函数的图象与坐标轴的交点分别为
，连接
（1）求
与
的值；
（2）求证： 
【答案】（1）
，
，b=1；（2）见解析．
【解析】
（1）先将点
代入反比例函数的解析式可得
的值，从而可求出点P的坐标，再利用待定系数法可求出
与b的值；
（2）先根据（1）可得一次函数的解析式，由此可得出点A、B的坐标，从而可得OA、OB的长，再根据等腰三角形的性质可得
，然后利用两点之间的距离公式可得OP、OQ的长，从而可得
，最后根据三角形全等的判定定理即可得证．
（1）将
代入反比例函数
得
，解得
则反比例函数的解析式为
将
代入反比例函数得
，解得
将，
代入一次函数
得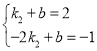
解得
综上，，，
；
（2）由（1）可知，一次函数解析式为
当
时，
当
时，
又
，
在
和
中，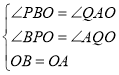
．
培优三好生系列答案
优化作业上海科技文献出版社系列答案
【题目】“垃圾分类就是新时尚”．树立正确的垃圾分类观念，促进青少年养成良好的文明习惯，对于增强公共意识，提升文明素质具有重要意义．为了调査学生对垃圾分类知识的了解情况，从甲、乙两校各随机抽取20名学生进行了相关知识测试，获得了他们的成绩（百分制，单位：分），并对数据（成绩）进行了整理、描述和分析，下面给出了部分信息．
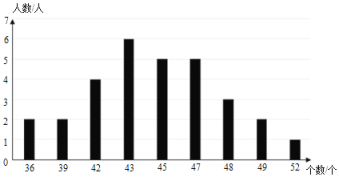
a．甲、乙两校学生样本成绩频数分布表及扇形统计图如下：
甲校学生样本成绩频数分布表（表1）
成绩m（分） | 频数 | 频率 |
|
| 0.10 |
|
|
|
| 4 | 0.20 |
| 7 | 0.35 |
| 2 |
|
合计 | 20 | 1.0 |
b．甲、乙两校学生样本成绩的平均分、中位数、众数、方差如下表所示：（表2）
学校 | 中位数 | 众数 | 方差 | |
甲 | 76.7 | 77 | 89 | 150.2 |
乙 | 78.1 | 80 |
| 135.3 |
其中，乙校20名学生样本成绩的数据如下：
54 72 62 91 87 69 88 79 80 62 80 84 93 67 87 87 90 71 68 91
请根据所给信息，解答下列问题：
（1）表1中
___________；表2中的众数
_________；
（2）乙校学生样本成绩扇形统计图（图1）中，
这一组成绩所在扇形的圆心角度数是_________度；
（3）在此次测试中，某学生的成绩是79分，在他所属学校排在前10名，由表中数据可知该学生是________校的学生（填“甲”或“乙”），理由是________________________；
（4）若乙校1000名学生都参加此次测试，成绩80分及以上为优秀，请估计乙校成绩优秀的学生约为________人．
