题目内容
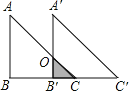
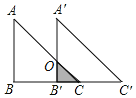
【题目】如图所示，已知Rt△ABC中，∠B＝90°，BC＝4，AB＝4，现将△ABC沿BC方向平移到△A′B′C′的位置．若平移的距离为3，则△ABC与△A′B′C′重叠部分的阴影面积为__．
【答案】
【解析】
依据平移的性质即可得出△B'OC是等腰直角三角形，再根据利用三角形面积公式可求重叠部分的阴影面积．
解：∵∠B＝90°，BC＝4，AB＝4，
∴△ABC是等腰直角三角形，
∴∠ACB＝45°，
∵△A′B′C′是△ABC平移得到的，
∴△ABC≌△A′B′C′，
∴∠B＝∠A′B′C′＝90°，
∴∠B'OC＝45°，
∴△B'OC是等腰直角三角形，
∵B'C＝BC﹣BB′＝4﹣3＝1，
∴S△B'OC＝×1×1＝，即S阴影＝，
故答案为：．
练习册系列答案
相关题目
