题目内容
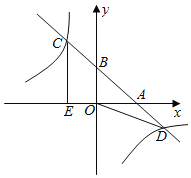
【题目】如图,直线y=﹣x+b与x、y轴的正半轴交于点A,B,与双曲线y=﹣![]() 交于点C(点C在第二象限内),点D,过点C作CE⊥x轴于点E,记四边形OBCE的面积为S1,△OBD的面积为S2,若
交于点C(点C在第二象限内),点D,过点C作CE⊥x轴于点E,记四边形OBCE的面积为S1,△OBD的面积为S2,若![]() =
=![]() ,则b的值为_____.
,则b的值为_____.
【答案】3
【解析】
根据双曲线的对称性得到BC=AD,设BC=AD=a,用a表示出点C和得D的坐标,根据梯形面积公式、三角形面积公式求出a、b的关系,根据反比例函数图象上点的坐标特征列出方程,解方程求出b.
解:由题意点B的坐标为(0,b),点A的坐标为(b,0),
∴OA=OB=b,
∵直线y=﹣x+b关于直线y=x对称,反比例函数y=﹣![]() 关于y=x对称,
关于y=x对称,
∴BC=AD,
设BC=AD=a,则C(﹣![]() a,b+
a,b+![]() a),D(b+
a),D(b+![]() a,﹣
a,﹣![]() a),
a),
∵![]() =
=![]() ,
,
∴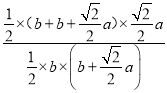 =
=![]() ,
,
整理得,12a2+17![]() ab﹣14b2=0,
ab﹣14b2=0,
解得,a1=![]() b,a2=﹣b(舍去),
b,a2=﹣b(舍去),
则D(![]() b,﹣
b,﹣![]() b),
b),
∴![]() b×(﹣
b×(﹣![]() b)=﹣4,
b)=﹣4,
解得,b1=3,b2=﹣3(舍去),
∴b=3,
故答案为:3.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
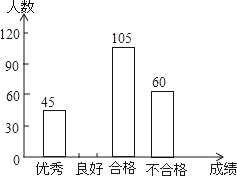
【题目】为了解今年初三学生的数学学习情况,某校对上学期的数学成绩作了统计分析,绘制得到如下图表.请结合图表所给出的信息解答下列问题:
成绩 | 频数 | 频率 |
优秀 | 45 | b |
良好 | a | 0.3 |
合格 | 105 | 0.35 |
不合格 | 60 | c |
(1)该校初三学生共有多少人?
(2)求表中a,b,c的值,并补全条形统计图.
(3)初三(一)班数学老师准备从成绩优秀的甲、乙、丙、丁四名同学中任意抽取两名同学做学习经验介绍,求恰好选中甲、乙两位同学的概率.