题目内容
【题目】对于平面直角坐标系![]() 中的点
中的点![]() 和图形
和图形![]() ,给出如下定义:若图形
,给出如下定义:若图形![]() 上存在两个点
上存在两个点![]() ,使得
,使得![]() 是边长为2的等边三角形,则称点
是边长为2的等边三角形,则称点![]() 是图形
是图形![]() 的一个“和谐点”.
的一个“和谐点”.
已知直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() 的半径为
的半径为![]() .
.
(1)若![]() ,在点
,在点![]() 中,直线
中,直线![]() 的和谐点是___________;
的和谐点是___________;
(2)若![]() 上恰好存在2个直线
上恰好存在2个直线![]() 的和谐点,求
的和谐点,求![]() 的取值范围;
的取值范围;
(3)若![]() ,线段
,线段![]() 上存在
上存在![]() 的和谐点,直接写出
的和谐点,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)结合定义,画图可知,当直线![]() 上的两点O,S与
上的两点O,S与![]() 或S,T与
或S,T与![]() 构成等边三角形,直线
构成等边三角形,直线![]() 的和谐点是
的和谐点是![]() ;
;
(2)由等边三角形的特征及直线![]() ,结合图形及对称性数形结合即可求解;
,结合图形及对称性数形结合即可求解;
(3)结合图形构造等边三角形知:分![]() 或
或![]() ,而
,而![]() 为定值,故关键求
为定值,故关键求![]() 的取值范围即可,进一步画图可知当
的取值范围即可,进一步画图可知当![]() 时,
时,![]() 最小,当
最小,当![]() 的和谐点恰好是
的和谐点恰好是![]() 点(即
点(即![]() 点与
点与![]() 点重合)时,
点重合)时,![]() 最大,分别计算即可得到
最大,分别计算即可得到![]() 的取值范围
的取值范围
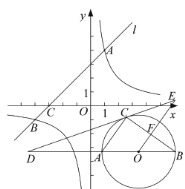
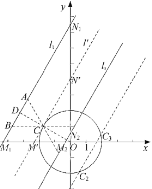
解:(1)直线![]() 的和谐点是
的和谐点是![]() ; 如图所示:
; 如图所示:
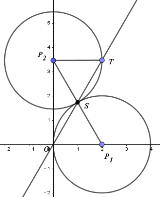
(2)如图,设![]() 在直线
在直线![]() 上,点
上,点![]() 在
在![]() 上,
上,![]() 是边长为2的等边三角形,
是边长为2的等边三角形,
![]() ,∴当直线
,∴当直线![]() 位于
位于![]() 时,
时,![]() 上只有1个点
上只有1个点![]() 是直线
是直线![]() 的和谐点,
的和谐点,
当直线![]() 位于
位于![]() 时,
时,![]() 上有3个点
上有3个点![]() 都是直线
都是直线![]() 的和谐点,
的和谐点,
∴满足条件的直线![]() 应位于直线
应位于直线![]() 和
和![]() 之间.
之间.
设过点![]() 且与
且与![]() 相切的直线为
相切的直线为![]() ,直线
,直线![]() 分别与
分别与![]() 轴,
轴,![]() 轴交于点
轴交于点![]() .连接
.连接![]() ,则
,则![]() .取
.取![]() 中点
中点![]() ,连接
,连接![]() ,则
,则![]() ,且
,且![]() 三点共线,
三点共线,![]() .
.
∵直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,
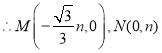 ,
,
![]() ,
,
![]() .
.
∴在![]() 和
和![]() 中,
中,
![]() ,
,
![]() ,
,
![]() ,
,
由对称性得![]() ,即
,即![]() ,
,
![]() 的取值范围是
的取值范围是![]() .
.
(3)![]() 的取值范围是
的取值范围是![]() .
.
详解如下:
![]() .
.
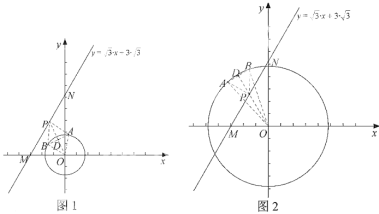
如图,设![]() 在
在![]() 上,
上,![]() 是
是![]() 上的点,
上的点,![]() 是边长为2的等边三角形,
是边长为2的等边三角形,
设![]() 的中点为
的中点为![]() ,则
,则![]() 三点共线,
三点共线,
![]() ,
,
又![]() (图1),或
(图1),或![]() (图2),而
(图2),而![]() 为定值,
为定值,
∴只需考虑![]() 的取值范围即可.
的取值范围即可.
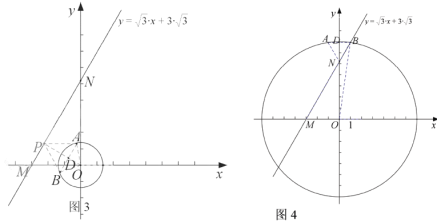
如图3,当![]() 时,
时,![]() 最小,此时
最小,此时![]() 的半径最小.
的半径最小.
![]() ,
,
![]() .
.
又![]() ,
,
![]() .
.
∴在![]() 中,
中,![]() ,
,
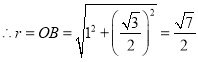 .
.
如图4,当![]() 的和谐点恰好是
的和谐点恰好是![]() 点(即
点(即![]() 点与
点与![]() 点重合)时,
点重合)时,![]() 最大,此时
最大,此时![]() 的半径最大,
的半径最大,
![]() ,
,
![]() ,
,
又![]() ,
,
![]() .
.
综上,![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目