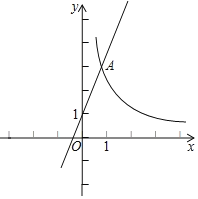题目内容
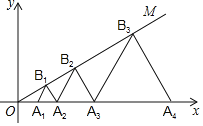
【题目】如图,在平面直角坐标系xOy的第一象限内依次作等边三角形△A1B1A2,△A2B2A3,△A3B3A4…,点A1,A2,A3,…,在x轴的正半轴上,点B1,B2,B3,…,在射线OM上,若∠B1OA1=30°,OA1=1,则点B2019坐标是_________ .
【答案】(3×22017,![]() ×22017)
×22017)
【解析】
由题意根据点的坐标规律,利用等边三角形的性质、勾股定理、锐角三角函数值即可求解.
解:根据题意得:等边三角形△A1B1A2,△A2B2A3,△A3B3A4…,
∵∠B1OA1=30°,OA1=1,
∠B1A1A2=∠A1A2B1=∠A2B1A1=60°,
∴∠OB1A1=30°,
∴∠OB1A2=90°,
∴A1A2=A2B1=A1B1=OA1=1,
所以B1 的横坐标为1+![]() =
=![]() ,纵坐标为
,纵坐标为![]() ×tan30°=
×tan30°=![]() ×
×![]() =
=![]() ;
;
同理可得:B2 的横坐标为2+1=3,纵坐标为3×![]() =
=![]() ;
;
B3 的横坐标为4+2=22+21,
B4 的横坐标为8+4=23+22,
B5 的横坐标为16+8=24+23,
…
Bn 的横坐标为2n﹣1+2n﹣2=2n﹣2(2+1)=3×2n﹣2,
纵坐标为3×2n﹣2×tan30°=![]() ×2n﹣2.
×2n﹣2.
所以B2019的坐标为(3×22017,![]() ×22017).
×22017).

【题目】如图1,小明用一张边长为![]() 的正方形硬纸板设计一个无盖的长方体纸盒,从四个角各剪去一个边长为
的正方形硬纸板设计一个无盖的长方体纸盒,从四个角各剪去一个边长为![]() 的正方形,再折成如图2所示的无盖纸盒,记它的容积为
的正方形,再折成如图2所示的无盖纸盒,记它的容积为![]() .
.
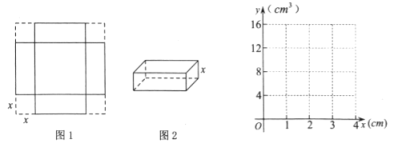
(1)![]() 关于
关于![]() 的函数表达式是__________,自变量
的函数表达式是__________,自变量![]() 的取值范围是___________.
的取值范围是___________.
(2)为探究![]() 随
随![]() 的变化规律,小明类比二次函数进行了如下探究:
的变化规律,小明类比二次函数进行了如下探究:
①列表:请你补充表格中的数据:
| 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 |
| 0 | 12.5 | 13.5 | 2.5 | 0 |
②描点:把上表中各组对应值作为点的坐标,在平面直角坐标系中描出相应的点;
③连线:用光滑的曲线顺次连结各点.
(3)利用函数图象解决:若该纸盒的容积超过![]() ,估计正方形边长
,估计正方形边长![]() 的取值范围.(保留一位小数)
的取值范围.(保留一位小数)
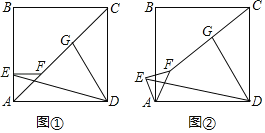
【题目】如图,五边形![]() 内部有若干个点,用这些点以及五边形
内部有若干个点,用这些点以及五边形![]() 的顶点
的顶点![]() 的顶点把原五边形分割成一些三角形(互相不重叠):
的顶点把原五边形分割成一些三角形(互相不重叠):

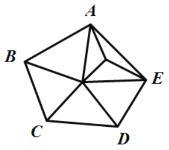
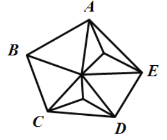
内部有1个点 内部有2个点 内部有3个点
(1)填写下表:
五边形 | 1 | 2 | 3 | 4 | … | n |
分割成的三角形的个数 | 5 | 7 | 9 | … |
(2)原五边形能否被分割成2019个三角形?若能,求此时五边形![]() 内部有多少个点?若不能,请说明理由.
内部有多少个点?若不能,请说明理由.