题目内容
【题目】如图,五边形![]() 内部有若干个点,用这些点以及五边形
内部有若干个点,用这些点以及五边形![]() 的顶点
的顶点![]() 的顶点把原五边形分割成一些三角形(互相不重叠):
的顶点把原五边形分割成一些三角形(互相不重叠):

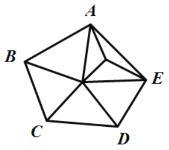
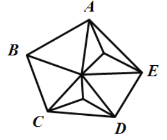
内部有1个点 内部有2个点 内部有3个点
(1)填写下表:
五边形 | 1 | 2 | 3 | 4 | … | n |
分割成的三角形的个数 | 5 | 7 | 9 | … |
(2)原五边形能否被分割成2019个三角形?若能,求此时五边形![]() 内部有多少个点?若不能,请说明理由.
内部有多少个点?若不能,请说明理由.
【答案】(1)详见解析;(2)1008
【解析】
(1)查出题干图形中三角形的个数,并观察发现,每多一个点,三角形的个数增加2,然后据此规律填表即可;
(2)根据(1)中规律,列式求解,如果n是整数,则能分割,如果不是整数,则不能分割.
(1)有1个点时,内部分割成5个三角形;
有2个点时,内部分割成5+2=7个三角形;
有3个点时,内部分割成5+2×2=9个三角形;
有4个点时,内部分割成6+2×3=11个三角形;
…
以此类推,有n个点时,内部分割成5+2×(n-1)=(2n+3)个三角形;
故可填表为:
五边形 | 1 | 2 | 3 | 4 | … |
|
分割成的三角形的个数 | 5 | 7 | 9 | 11 | … |
|
(2)可以,
令![]() ,解得
,解得![]() .
.
∴此时正方形ABCD内部有1008个点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】“十一”黄金周,坚胜家电城大力促销,收银情况一直看好![]() 下表为当天与前一天的营业额的涨跌情况
下表为当天与前一天的营业额的涨跌情况![]() 已知9月30日的营业额为26万元.
已知9月30日的营业额为26万元.
10月1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
4 | 3 | 2 | 0 |
|
|
|
![]() 黄金周内收入最低的哪一天?
黄金周内收入最低的哪一天?![]() 直接回答,不必写过程
直接回答,不必写过程![]() .
.
![]() 黄金周内平均每天的营业额是多少?
黄金周内平均每天的营业额是多少?