ÌâÄ¿ÄÚÈÝ
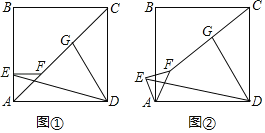
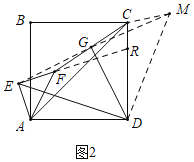
¡ŸÌâÄ¿¡¿ÈçÍŒ£¬ËıßÐÎABCDΪÕý·œÐΣ¬¡÷AEFΪµÈÑüÖ±œÇÈýœÇÐΣ¬¡ÏAEF£œ90¡ã£¬Á¬œÓFC£¬GΪFCµÄÖе㣬Á¬œÓGD£¬ED£®
£š1£©ÈçÍŒ¢Ù£¬EÔÚABÉÏ£¬Ö±œÓÐŽ³öED£¬GDµÄÊýÁ¿¹Øϵ£®
£š2£©œ«ÍŒ¢ÙÖеġ÷AEFÈƵãAÄæʱÕëÐýת£¬ÆäËüÌõŒþ²»±ä£¬ÈçÍŒ¢Ú£¬£š1£©ÖеĜáÂÛÊÇ·ñ³ÉÁ¢£¿ËµÃ÷ÀíÓÉ£®
£š3£©ÈôAB£œ5£¬AE£œ1£¬œ«ÍŒ¢ÙÖеġ÷AEFÈƵãAÄæʱÕëÐýתһÖÜ£¬µ±E£¬F£¬CÈýµã¹²Ïßʱ£¬Ö±œÓÐŽ³öEDµÄ³€£®
¡ŸŽð°ž¡¿£š1£©DE£œ![]() DG£»£š2£©³ÉÁ¢£¬ÀíÓÉŒûœâÎö£»£š3£©DEµÄ³€Îª4
DG£»£š2£©³ÉÁ¢£¬ÀíÓÉŒûœâÎö£»£š3£©DEµÄ³€Îª4![]() »ò3
»ò3![]() £®
£®
¡ŸœâÎö¡¿
£š1£©žùŸÝÌâÒâœáÂÛ£ºDE=![]() DG£¬ÈçÍŒ1ÖУ¬Á¬œÓEG£¬ÑÓ³€EGœ»BCµÄÑÓ³€ÏßÓÚM£¬Á¬œÓDM£¬Ö€Ã÷¡÷CMG¡Õ¡÷FEG£šAAS£©£¬ÍƳöEF=CM£¬GM=GE£¬ÔÙÖ€Ã÷¡÷DCM¡Õ¡÷DAE£šSAS£©ŒŽ¿ÉœâŸöÎÊÌ⣻
DG£¬ÈçÍŒ1ÖУ¬Á¬œÓEG£¬ÑÓ³€EGœ»BCµÄÑÓ³€ÏßÓÚM£¬Á¬œÓDM£¬Ö€Ã÷¡÷CMG¡Õ¡÷FEG£šAAS£©£¬ÍƳöEF=CM£¬GM=GE£¬ÔÙÖ€Ã÷¡÷DCM¡Õ¡÷DAE£šSAS£©ŒŽ¿ÉœâŸöÎÊÌ⣻
£š2£©ÈçÍŒ2ÖУ¬œáÂÛ³ÉÁ¢£®Á¬œÓEG£¬ÑÓ³€EGµœM£¬Ê¹µÃGM=GE£¬Á¬œÓCM£¬DM£¬ÑÓ³€EFœ»CDÓÚR£¬ÆäÖ€Ã÷·œ·šÀàËÆ£»
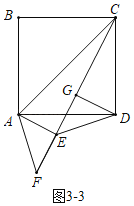
£š3£©ÓÉÌâÒâ·ÖÁœÖÖÇéÐΣº¢ÙÈçÍŒ3-1ÖУ¬µ±E£¬F£¬C¹²Ïßʱ£®¢ÚÈçÍŒ3-3ÖУ¬µ±E£¬F£¬C¹²Ïßʱ£¬·Ö±ðÇóœâŒŽ¿É£®
œâ£º£š1£©œáÂÛ£ºDE£œ![]() DG£®
DG£®
ÀíÓÉ£ºÈçÍŒ1ÖУ¬Á¬œÓEG£¬ÑÓ³€EGœ»BCµÄÑÓ³€ÏßÓÚM£¬Á¬œÓDM£®
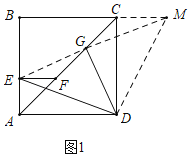
¡ßËıßÐÎABCDÊÇÕý·œÐΣ¬
¡àAD£œCD£¬¡ÏB£œ¡ÏADC£œ¡ÏDAE£œ¡ÏDCB£œ¡ÏDCM£œ90¡ã£¬
¡ß¡ÏAEF£œ¡ÏB£œ90¡ã£¬
¡àEF¡ÎCM£¬
¡à¡ÏCMG£œ¡ÏFEG£¬
¡ß¡ÏCGM£œ¡ÏEGF£¬GC£œGF£¬
¡à¡÷CMG¡Õ¡÷FEG£šAAS£©£¬
¡àEF£œCM£¬GM£œGE£¬
¡ßAE£œEF£¬
¡àAE£œCM£¬
¡à¡÷DCM¡Õ¡÷DAE£šSAS£©£¬
¡àDE£œDM£¬¡ÏADE£œ¡ÏCDM£¬
¡à¡ÏEDM£œ¡ÏADC£œ90¡ã£¬
¡àDG¡ÍEM£¬DG£œGE£œGM£¬
¡à¡÷EGDÊǵÈÑüÖ±œÇÈýœÇÐΣ¬
¡àDE£œ![]() DG£®
DG£®
£š2£©ÈçÍŒ2ÖУ¬œáÂÛ³ÉÁ¢£®
ÀíÓÉ£ºÁ¬œÓEG£¬ÑÓ³€EGµœM£¬Ê¹µÃGM£œGE£¬Á¬œÓCM£¬DM£¬ÑÓ³€EFœ»CDÓÚR£®
¡ßEG£œGM£¬FG£œGC£¬¡ÏEGF£œ¡ÏCGM£¬
¡à¡÷CGM¡Õ¡÷FGE£šSAS£©£¬
¡àCM£œEF£¬¡ÏCMG£œ¡ÏGEF£¬
¡àCM¡ÎER£¬
¡à¡ÏDCM£œ¡ÏERC£¬
¡ß¡ÏAER+¡ÏADR£œ180¡ã£¬
¡à¡ÏEAD+¡ÏERD£œ180¡ã£¬
¡ß¡ÏERD+¡ÏERC£œ180¡ã£¬
¡à¡ÏDCM£œ¡ÏEAD£¬
¡ßAE£œEF£¬
¡àAE£œCM£¬
¡à¡÷DAE¡Õ¡÷DCM£šSAS£©£¬
¡àDE£œDM£¬¡ÏADE£œ¡ÏCDM£¬
¡à¡ÏEDM£œ¡ÏADC£œ90¡ã£¬
¡ßEG£œGM£¬
¡àDG£œEG£œGM£¬
¡à¡÷EDGÊǵÈÑüÖ±œÇÈýœÇÐΣ¬
¡àDE£œ![]() DG£®
DG£®
£š3£©¢ÙÈçÍŒ3©1ÖУ¬µ±E£¬F£¬C¹²Ïßʱ£¬
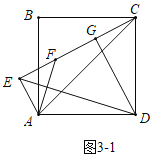
ÔÚRt¡÷ADCÖУ¬AC£œ![]() £œ
£œ![]() £œ5
£œ5![]() £¬
£¬
ÔÚRt¡÷AECÖУ¬EC£œ![]() £œ
£œ![]() £œ7£¬
£œ7£¬
¡àCF£œCE©EF£œ6£¬
¡àCG£œ![]() CF£œ3£¬
CF£œ3£¬
¡ß¡ÏDGC£œ90¡ã£¬
¡àDG£œ![]() £œ
£œ![]() £œ4£¬
£œ4£¬
¡àDE£œ![]() DG£œ4
DG£œ4![]() £®
£®
¢ÚÈçÍŒ3©3ÖУ¬µ±E£¬F£¬C¹²Ïßʱ£¬Í¬·š¿ÉµÃDE£œ3![]() £®
£®
×ÛÉÏËùÊö£¬DEµÄ³€Îª4![]() »ò3
»ò3![]() £®
£®

¡ŸÌâÄ¿¡¿¹úŒÒœÌÓý²¿Ìá³ö¡°Ã¿Ìì¶ÍÁ¶Ò»Ð¡Ê±£¬œ¡¿µ¹€×÷ÎåÊ®Ä꣬ÐÒž£Éú»îÒ»±²×Ó¡±.ÍòÖÝÇøijÖÐѧ¶ÔŸÅÄꌶ²¿·ÖѧÉúœøÐÐÎÊŸíµ÷²é¡°Äã×îϲ»¶µÄ¶ÍÁ¶ÏîÄ¿ÊÇʲΣ¿¡±£¬¹æ¶šŽÓ¡°ŽòÇò¡±£¬¡°Åܲœ¡±£¬¡°ÓÎÓŸ¡±£¬¡°ÌøÉþ¡±£¬¡°ÆäËû¡±ÎåžöÑ¡ÏîÖÐÑ¡Ôñ×ÔŒº×îϲ»¶µÄÏîÄ¿£¬ÇÒÖ»ÄÜÑ¡ÔñÒ»žöÏîÄ¿£¬²¢œ«µ÷²éœá¹û»æÖƳÉÈçÏÂÁœ·ù²»ÍêÕûµÄͳŒÆÍŒ.
×îϲ»¶µÄ¶ÍÁ¶ÏîÄ¿ | ÈËÊý |
ŽòÇò | 120 |
Åܲœ |
|
ÓÎÓŸ |
|
ÌøÉþ | 30 |
ÆäËû |
|
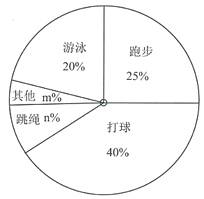
£š1£©ÕâŽÎÎÊŸíµ÷²éµÄѧÉú×ÜÈËÊýΪ £¬ÈËÊý![]() £»
£»
£š2£©ÉÈÐÎͳŒÆÍŒÖУ¬![]() £¬¡°ÆäËû¡±¶ÔÓŠµÄÉÈÐεÄÔ²ÐĜǵĶÈÊýΪ ¶È£»
£¬¡°ÆäËû¡±¶ÔÓŠµÄÉÈÐεÄÔ²ÐĜǵĶÈÊýΪ ¶È£»
£š3£©ÈôžÃÄꌶÓÐ1200ÃûѧÉú£¬¹ÀŒÆϲ»¶¡°ÌøÉþ¡±ÏîÄ¿µÄѧÉúŽóÔŒÓжàÉÙÈË£¿