Question

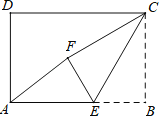
【题目】如图，在矩形ABCD中，AB=3，CB=2，点E为线段AB上的动点，将△CBE沿CE折叠，使点B落在矩形内点F处，下列结论正确的是_____（写出所有正确结论的序号）

①当E为线段AB中点时，AF∥CE；

②当E为线段AB中点时，AF=；

③当A、F、C三点共线时，AE=；

④当A、F、C三点共线时，△CEF≌△AEF．

Answer 1

【答案】①②③

【解析】分两种情形分别求解即可解决问题；

如图1中，当AE=EB时，

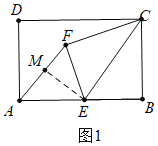
∵AE=EB=EF，

∴∠EAF=∠EFA，

∵∠CEF=∠CEB，∠BEF=∠EAF+∠EFA，

∴∠BEC=∠EAF，

∴AF∥EC，故①正确，

作EM⊥AF，则AM=FM，

在Rt△ECB中，EC=，

∵∠AME=∠B=90°，∠EAM=∠CEB，

∴△CEB∽△EAM，

∴，

∴，

∴AM=，

∴AF=2AM=，故②正确，

如图2中，当A、F、C共线时，设AE=x．

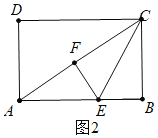
则EB=EF=3-x，AF=-2，

在Rt△AEF中，∵AE2=AF2+EF2，

∴x2=（-2）2+（3-x）2，

∴x=，

∴AE=，故③正确，

如果，△CEF≌△AEF，则∠EAF=∠ECF=∠ECB=30°，显然不符合题意，故④错误，

故答案为①②③．