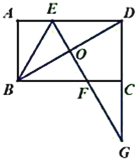
题目内容
【题目】在平面直角坐标系xOy,对于点P(xp,yp)和图形G,设Q(xQ,yQ)是图形G上任意一点,|xp﹣xQ|的最小值叫点P和图形G的“水平距离”,|yp﹣yQ|的最小值叫点P和图形G的“竖直距离”,点P和图形G的“水平距离”与“竖直距离”的最大值叫做点P和图形G的“绝对距离”
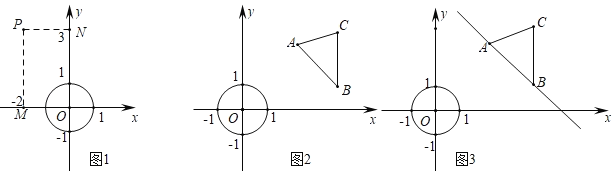
例如:点P(﹣2,3)和半径为1的⊙O,因为⊙O上任一点Q(xQ,yQ)满足﹣1≤xQ≤1,﹣1≤yQ≤1,点P和⊙O的“水平距离”为|﹣2﹣xQ|的最小值,即|﹣2﹣(﹣1)|=1,点P和⊙O的“竖直距离”为|3﹣yQ|的最小值即|3﹣1|=2,因为2>1,所以点P和⊙O的“绝对距离”为2.
已知⊙O半径为1,A(2,![]() ),B(4,1),C(4,3)
),B(4,1),C(4,3)
(1)①直接写出点A和⊙O的“绝对距离”
②已知D是△ABC边上一个动点,当点D与⊙O的“绝对距离”为2时,写出一个满足条件的点D的坐标;
(2)已知E是△ABC边一个动点,直接写出点E与⊙O的“绝对距离”的最小值及相应的点E的坐标
(3)已知P是⊙O上一个动点,△ABC沿直线AB平移过程中,直接写出点P与△ABC的“绝对距离”的最小值及相应的点P和点C的坐标.
【答案】(1)①1.5;②D的坐标为(3,![]() )或(3,
)或(3,![]() );(2)E坐标为(
);(2)E坐标为(![]() ,
,![]() );(3)C(
);(3)C(![]() ,
,![]() ),P(
),P(![]() ,
,![]() ).点P与△ABC的“绝对距离”的最小值为
).点P与△ABC的“绝对距离”的最小值为![]() .
.
【解析】
(1)①点A和⊙O的“绝对距离”的定义求出点A和⊙O的“竖直距离”与“水平距离”即可解决问题.
②当点D与⊙O的“绝对距离”为2时,点D的横坐标为3,求出直线AB,AC的解析式即可解决问题.
(2)由题意可知满足条件的点E在直线y=x与直线AB的交点处.构建方程组即可解决问题.
(3)如图3中,过点A作x轴的垂线,过点B作y轴的垂线交于点F,当点F在直线y=x上时,点P与△ABC的“绝对距离”的有最小值,此时点P即为直线y=x与⊙O的交点(如图所示).设F(m,m)则B(m+2,m),利用待定系数法求出点F的坐标即可解决问题.
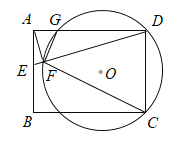
(1)如图1中,
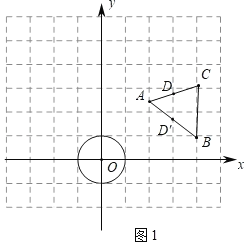
①∵点A和⊙O的“水平距离”是1,点A和⊙O的“竖直距离”是1.5,
又∵1.5>1,∴点A和⊙O的“绝对距离”是1.5.
②当点D与⊙O的“绝对距离”为2时,点D的横坐标为3.
∵A(2,![]() ),B(4,1),C(4,3),
),B(4,1),C(4,3),
∴直线AB速度解析式为y![]() x+4,直线AC的解析式为y
x+4,直线AC的解析式为y![]() x+2,
x+2,
∴D(3,![]() ),D'(3,
),D'(3,![]() ),
),
综上所述:满足条件的点D的坐标为(3,![]() )或(3,
)或(3,![]() ).
).
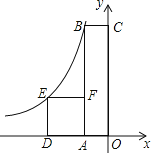
(2)如图2中,

由题意可知满足条件的点E在直线y=x与直线AB的交点处.
由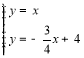 ,解得
,解得![]() ,
,
∴满足条件的点E坐标为(![]() ,
,![]() ).
).
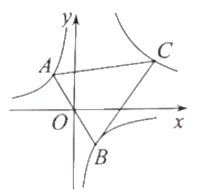
(3)如图3中,过点A作x轴的垂线,过点B作y轴的垂线交于点F,当点F在直线y=x上时,点P与△ABC的“绝对距离”的有最小值,此时点P即为直线y=x与⊙O的交点(如图所示).
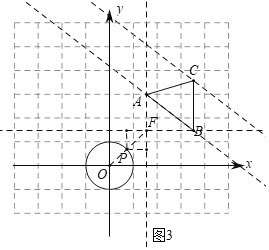
设F(m,m)则B(m+2,m).
∵点B在直线y![]() x+4上,
x+4上,
∴m![]() (m+2)+4,
(m+2)+4,
解得:m![]() ,
,
∴F(![]() ,
,![]() ),B(
),B(![]() ,
,![]() ).
).
∵BC∥y轴,BC=2,
∴C(![]() ,
,![]() ),此时P(
),此时P(![]() ,
,![]() ).
).
∴点P与△ABC的“绝对距离”的最小值为![]() .
.

【题目】某商场甲、乙、丙三名业务员2018年前5个月的销售额(单位:万元)如下表:
月份 销售额 人员 | 第1月 | 第2月 | 第3月 | 第4月 | 第5月 |
甲 | 6 | 9 | 10 | 8 | 8 |
乙 | 5 | 7 | 8 | 9 | 9 |
丙 | 5 | 9 | 10 | 5 | 11 |
(1)根据上表中的数据,将下表补充完整:
统计值 数值 人员 | 平均数(万元) | 众数(万元) | 中位数(万元) | 方差 |
甲 | 8 | 8 | 1.76 | |
乙 | 7.6 | 8 | 2.24 | |
丙 | 8 | 5 |
(2)甲、乙、丙三名业务员都说自己的销售业绩好,你赞同谁的说法?请说明理由.