Question

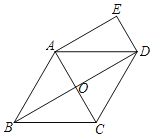
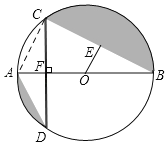
【题目】如图，AB为⊙O直径，OE⊥BC垂足为E，AB⊥CD垂足为F．

（1）求证：AD＝2OE；

（2）若∠ABC＝30°，⊙O的半径为2，求两阴影部分面积的和．

Answer 1

【答案】（1）见解析；（2）2π﹣2

【解析】

（1）连接AC，由垂径定理得弧AC=弧AD，从而AC＝AD，又OE⊥BC，则E为BC的中点，所以OE是△ABC的中位线，由中位线的性质可得OE＝AC，从而可证AD＝2OE；

（2）根据S阴影＝S半圆﹣S△ABC求解即可.

解：（1）证明：连接AC，

∵AB⊥CD，

∴弧AC=弧AD，

∴AC＝AD，

∵OE⊥BC，

∴E为BC的中点，

∵O为AB的中点，

∴OE 为△ABC的中位线，

∴OE＝AC，

∴OE＝AD，

即AD＝2OE；

（2）S半圆＝πOB2＝＝2π，

∵AB为⊙O直径，

∴∠ACB＝90°，

∵∠ABC＝30°，AB＝4，

∴AC＝AB＝，

BC＝，

S△ABC＝ACBC＝＝2，

∵AB⊥CD，

∴拱形AD的面积＝弓形AC的面积，

∴S阴影＝S半圆﹣S△ABC＝2π﹣2．