题目内容
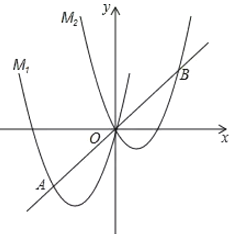
【题目】如图,在平面直角坐标系xOy中,函数y![]() (x>0)的图象与直线y=2x+1交于点A(1,m)
(x>0)的图象与直线y=2x+1交于点A(1,m)
(1)求k,m的值;
(2)已知点P(0,n)(n>0),过点P作平行于x轴的直线,交直线y=2x+1于点B,交函数y![]() (x>0)的图象于点C.横、纵坐标都是整数的点叫做整点.
(x>0)的图象于点C.横、纵坐标都是整数的点叫做整点.
①当n=1时,写出线段BC上的整点的坐标;
②若y![]() (x>0)的图象在点A,C之间的部分与线段AB,BC所围成的区域内(包括边界)恰有6个整点,直接写出n的取值范围.
(x>0)的图象在点A,C之间的部分与线段AB,BC所围成的区域内(包括边界)恰有6个整点,直接写出n的取值范围.
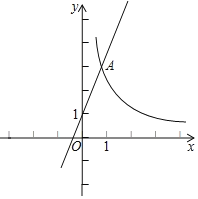
【答案】(1)k=3,m=3;(2)①线段BC上有(0,1)、(1,1)、(2,1)、(3,1)共4个整点;②0<n≤1或6≤n<7.
【解析】
(1)将A点代入直线解析式可求m,再代入y![]() ,可求k;
,可求k;
(2)①根据题意先求B,C两点,可得线段BC上的整点的横坐标的范围0≤x≤3,且x为整数,所以x取0,1,2,3.即求出整点个数.
②根据图象可以直接判断0<n≤1时或6≤n<7.
(1)∵点A(1,m)在y=2x+1上,∴m=2×1+1=3,∴A(1,3).
∵点A(1,3)在函数y![]() (x>0)的图象上,∴k=3.
(x>0)的图象上,∴k=3.
(2)①当n=1时,B、C两点的坐标为B(0,1)、C(3,1).
∵整点在线段BC上,∴0≤x≤3且x为整数,∴x=0,1,2,3,∴线段BC上有(0,1)、(1,1)、(2,1)、(3,1)共4个整点.
②
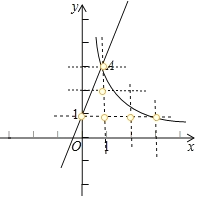
由图象可得当0<n≤1时或6≤n<7,有6个整点.

练习册系列答案
相关题目