题目内容
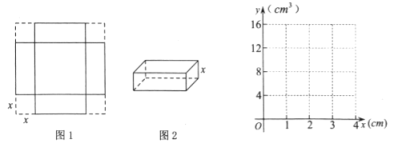
【题目】如图1,小明用一张边长为![]() 的正方形硬纸板设计一个无盖的长方体纸盒,从四个角各剪去一个边长为
的正方形硬纸板设计一个无盖的长方体纸盒,从四个角各剪去一个边长为![]() 的正方形,再折成如图2所示的无盖纸盒,记它的容积为
的正方形,再折成如图2所示的无盖纸盒,记它的容积为![]() .
.
(1)![]() 关于
关于![]() 的函数表达式是__________,自变量
的函数表达式是__________,自变量![]() 的取值范围是___________.
的取值范围是___________.
(2)为探究![]() 随
随![]() 的变化规律,小明类比二次函数进行了如下探究:
的变化规律,小明类比二次函数进行了如下探究:
①列表:请你补充表格中的数据:
| 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 |
| 0 | 12.5 | 13.5 | 2.5 | 0 |
②描点:把上表中各组对应值作为点的坐标,在平面直角坐标系中描出相应的点;
③连线:用光滑的曲线顺次连结各点.
(3)利用函数图象解决:若该纸盒的容积超过![]() ,估计正方形边长
,估计正方形边长![]() 的取值范围.(保留一位小数)
的取值范围.(保留一位小数)
【答案】(1)![]() ,
,![]() ;(2)①16,8;②见解析;③见解析;(3)
;(2)①16,8;②见解析;③见解析;(3)![]() (或
(或![]() )
)
【解析】
(1)先根据已知条件用含x的式子表示出长方体底面边长,再乘以长方体的高即可;
(2)①根据(1)得出的关系式求当x=1、2时对应的y的值补充表格;②③根据描点法画出函数图像即可;
(3)根据图像知y=12时,x的值由两个,再估算x的值,再根据图像由y>12,得出x的取值范围即可.
解:(1)由题意可得,无盖纸盒的底面是一个正方形,且边长为(6-2x)cm,
∴![]() ,
,
x的取值范围为:0<6-2x<6,解得![]() .
.
故答案为:![]() ;
;![]() ;
;
(2)①当x=1时,y=4-24+36=16;当x=2时,y=4×8-24×4+36×2=8;
故答案为:16,8;
②③如图所示:

(3)由图像可知,当y=12时,0<x<1,或1<x<2,
①当0<x<1时,
当x=0.4时,y=10.816,当x=0.5时,y=12.5,∴当y=12时,x≈0.5(或0.4);
②当1<x<2时,
当x=1.6时,y=12.544,当x=1.7时,y=11.492,∴当y=12时,x≈1.6(或1.7),
∴当y>12时,x的取值范围是![]() (或
(或![]() ).
).

 阅读快车系列答案
阅读快车系列答案【题目】小明对![]() ,
,![]() ,
,![]() ,
,![]() 四个中小型超市的女工人数进行了统计,并绘制了下面的统计图表,已知
四个中小型超市的女工人数进行了统计,并绘制了下面的统计图表,已知![]() 超市有女工20人.所有超市女工占比统计表
超市有女工20人.所有超市女工占比统计表
超市 |
|
|
|
|
女工人数占比 | 62.5% | 62.5% | 50% | 75% |
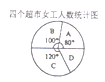
(1)![]() 超市共有员工多少人?
超市共有员工多少人?![]() 超市有女工多少人?
超市有女工多少人?
(2)若从这些女工中随机选出一个,求正好是![]() 超市的概率;
超市的概率;
(3)现在![]() 超市又招进男、女员工各1人,
超市又招进男、女员工各1人,![]() 超市女工占比还是75%吗?甲同学认为是,乙同学认为不是.你认为谁说的对,并说明理由.
超市女工占比还是75%吗?甲同学认为是,乙同学认为不是.你认为谁说的对,并说明理由.
【题目】某电器超市销售每台进价分别为2000元、1700元的A、B两种型号的空调,如表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 18000元 |
第二周 | 4台 | 10台 | 31000元 |
(进价、售价均保持不变,利润=销售总收入进货成本)
(1)求A、B两种型号的空调的销售单价;
(2)若超市准备用不多于54000元的金额再采购这两种型号的空调共30台,求A种型号的空调最多能采购多少台?