题目内容
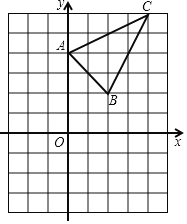
【题目】如图,在平面直角坐标系中,已知![]() ,
,![]() ,点
,点![]() 从
从![]() 点开始沿
点开始沿![]() 边向点
边向点![]() 以
以![]() 的速度移动;点
的速度移动;点![]() 从点
从点![]() 开始沿
开始沿![]() 边向点
边向点![]() 以
以![]() 的速度移动,如果
的速度移动,如果![]() 、
、![]() 同时出发,用
同时出发,用![]() 表示移动的时间
表示移动的时间![]() ,那么:
,那么:
(1)设![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数解析式.
的函数解析式.
(2)当![]() 的面积最大时,
的面积最大时,![]() 沿直线
沿直线![]() 翻折后得到
翻折后得到![]() ,试判断点
,试判断点![]() 是否落在直线
是否落在直线![]() 上,并说明理由.
上,并说明理由.
(3)当为![]() 何值时,
何值时,![]() 与
与![]() 相似?
相似?
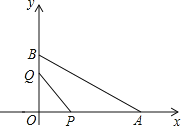
【答案】(1)![]() ;(2)点
;(2)点![]() 不落在直线
不落在直线![]() 上,理由见解析;(3)当
上,理由见解析;(3)当![]() 或
或![]() 时,
时,![]() 与
与![]() 相似.
相似.
【解析】
(1)根据P、Q的速度,用时间t表示出OQ和OP的长,即可通过三角形的面积公式得出y,t的函数关系式;
(2)先根据(1)的函数式求出y最大时,x的值,即可得出OQ和OP的长,然后求出C点的坐标和直线AB的解析式,将C点坐标代入直线AB的解析式中即可判断出C是否在AB上;
(3)本题要分△OPQ∽△OAB和△OPQ∽△OBA两种情况进行求解,可根据各自得出的对应边成比例求出t的值.
(1)![]()
由题意,得![]()
![]() ,
,
![]()
(2)![]()
![]() 当
当![]() 有最大值时,
有最大值时,![]()
![]() 即
即![]() 是等腰直角三角形.
是等腰直角三角形.
把![]() 沿
沿![]() 翻折后,可得四边形
翻折后,可得四边形![]() 是正方形,如图所示,
是正方形,如图所示,
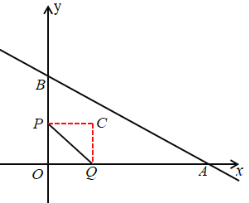
![]() 点
点![]() 的坐标是
的坐标是![]()
![]() ,
,![]() ,
,
![]() 直线
直线![]() 的解析式为
的解析式为![]() ,
,
当![]() 时,
时,![]() ,
,
![]() 点
点![]() 不落在直线
不落在直线![]() 上.
上.
(3)①若△OPQ∽△OAB,则有 ![]() ,
,
即![]() ,
,![]() ,
,
![]() .
.
②若△OPQ∽△OBA ,则有![]() ,
,
即![]() ,
,
![]() .
.
![]() 当
当![]() 或
或![]() 时,
时,![]() 与
与![]() 相似.
相似.

练习册系列答案
相关题目