题目内容
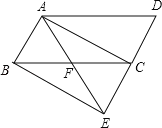
【题目】如图,已知正方形ABCD的边长为5,点E、F分别在BC和CD边上,分别连接AE、AF、EF,若∠EAF=45°,则△CEF的周长是( )

A.6+2![]() B.8.5C.10D.12
B.8.5C.10D.12
【答案】C
【解析】
将△ABE绕点A逆时针旋转90°得到△ADH,根据旋转的性质可得HD=BE,AH=AE,∠DAH=∠BAE,然后求出∠FAH=∠EAF,再利用“边角边”证明△AEF和△AHF全等,根据全等三角形对应边相等可得EF=FH,然后求出△CEF的周长=BC+CD,再根据正方形的边长求解即可.
解:如图,将△ABE绕点A逆时针旋转90°得到△ADH,
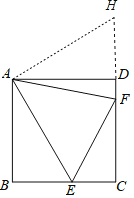
由旋转的性质得,HD=BE,AH=AE,∠DAH=∠BAE,
所以,∠FAH=∠DAH+∠DAF=∠BAE+∠DAF=∠BAD﹣∠EAF=90°﹣∠EAF,
∵∠EAF=45°,
∴∠FAH=90°﹣45°=45°,
∴∠FAH=∠EAF,
在△AEF和△AHF中,
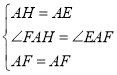 ,
,
∴△AEF≌△AHF(SAS),
∴EF=FH,
∴△CEF的周长=EF+CF+CE,
=FH+CF+CE,
=FD+DH+CF+CE,
=DF+BE+CF+CE,
=(BE+CE)+(DF+CF),
=BC+CD,
∵正方形ABCD的边长为5,
∴△CEF的周长为5+5=10
故选:C.

练习册系列答案
相关题目
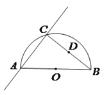
【题目】如图,AB是半圆O的直径,AB=10,过点A的直线交半圆于点C,且sin∠CAB=![]() ,连结BC,点D为BC的中点.已知点E在射线AC上,△CDE与△ACB相似,则线段AE的长为________;
,连结BC,点D为BC的中点.已知点E在射线AC上,△CDE与△ACB相似,则线段AE的长为________;